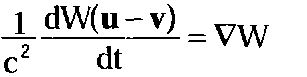(4.17.1)

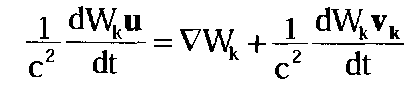(4.17.2)

297

где Wk — функция полевой связи исследуемой частицы с каждым отдельным источником, a vk — его скорость в данной системе отсчета.

Движение исследуемой частицы в данном случае определяется совокупностью всех таких уравнений:

x?^?VWi+x?M^ (4,,3)

В этом уравнении мы видим полную массу исследуемой частицы М:

M = -l^t=H^ (4.17.4)

k L к

Полную силу F, действующую со стороны всех полей:

F~z™i=i4, (4175)

И наконец, набор сил инерции для каждой компоненты полевой среды, которые выражаются последним слагаемым в правой части. В итоге мы получаем полевое уравнение движения для многокомпонентной полевой среды, описывающей движение исследуемой частицы под влиянием большого количества произвольно движущихся источников:

Полевое уравнение движения для многокомпонентной полевой среды

Это уравнение ярко демонстрирует суть всей полевой механики. И ее принципиальное отличие как от классической, так и от релятивистской физики. Полевое уравнение движения приобретает наиболее простой вид, идентичный второму закону Ньютона, только при отсутствии всех полевых сил инерции:

^ = F (4.17.7)

Вообще говоря, это оказывается возможным при выполнении условия

Lik vk = const для всех компонент полевой среды. Однако на практике, учитывая независимость изменения величины полевой массы и скорости частицы-источника относительно произвольно выбранной системы отсчета, дополнительными силами инерции можно пренебречь только в

298

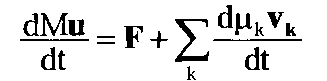двух случаях. Первым является классическое приближение, в рамках

которого считается, что все ixk = 0. Это условие находится в пределах погрешности экспериментов и является вполне применимым для более слабого гравитационного поля, но уже никак не подходит для электричества. Это и привело к возникновению проблем классической механики по мере развития электромагнетизма.

Вторым случаем является выполнение условия vk = 0, задающее выделенную систему отсчета. В этой системе отсчета уравнение движения приобретает наиболее простой вид второго закона Ньютона. Фактически это условие приводит нас к системе поля, которая в классическом понимании как раз и несет смысл инерциальной системы отсчета. Но в случае подвижного источника полевое уравнение движения уже не совпадает со вторым законом Ньютона, и в нем появляются дополнительные слагаемые. Эти слагаемые имеют структуру сил инерции и определяются скоростью движения данного источника, а также величиной полевой массы, обусловленной взаимодействием с ним исследуемой частицы.