Вот как просто все оказалось! И никаких преобразований Лоренца. Никакого замедления времени. Никакого сокращения длин. И никаких искусственных изобретений, вроде инерциальных систем отсчета или импульса поля. Все дело в одной маленькой поправке — полевой центробежной силе, естественным образом корректирующей магнитную силу при переходе из одной системы отсчета в другую!

296

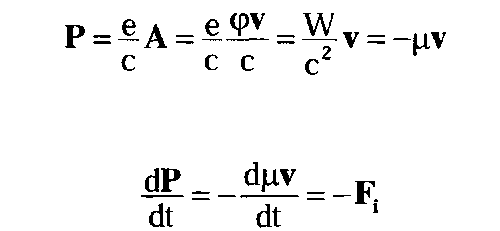4.17. Принцип относительности

или крах инерциальных систем отсчета

Мы решили проблему относительности! Конечно же, все оказалось несколько сложнее, чем представлялось нам в начале, в первой главе. Хотя по-другому быть и не могло. Ведь мы разгадали величайшую загадку физики. Загадку, создавшую жуткую путаницу в науке с конца XIX века и вплоть до наших дней.

Теперь можно подвести некий итог всему сказанному выше. А именно, собрать воедино весь алгоритм, позволяющий на основании полевой механики описать произвольное движение заряженных частиц в любой системе отсчета. Сделаем это.

В отличие от классической и современной физики мы больше не используем понятие инерциальной системы отсчета. А рассматриваем совершенно произвольную систему, которая может двигаться как угодно. В этой системе отсчета нас интересует описание движения исследуемой частицы, скорость которой равна U. При этом исследуемая частица взаимодействует с другой частицей, называемой источником, которая движется в данной системе отсчета со скоростью V .

Полевое уравнение движения исследуемой частицы является инвариантным и имеет вид:

Функция плотности полевой среды W в окрестностях частицы регистрации определяется положением обеих частиц, а точнее их относительным расстоянием, и несет логический смысл функции полевой связи. Ее классическим аналогом является потенциальная энергия взаимодействия или скалярный потенциал.

Часто оказывается, что источников полей несколько, и все они движутся различным образом. Это приводит к образованию многокомпонентной полевой среды, которую, вообще говоря, нельзя разделить на отдельные попарные взаимодействия. В этом случае движение становится квантовым и требует отдельного изучения. Но если же компоненты полевой среды являются независимыми (по крайней мере, в первом приближении), то для каждой компоненты мы можем записать аналогичное полевое уравнение движения: