Этот же результат мы получим и в системе отсчета, в которой обе частицы движутся. Потому что при взаимоперпендикулярном движении по-

294

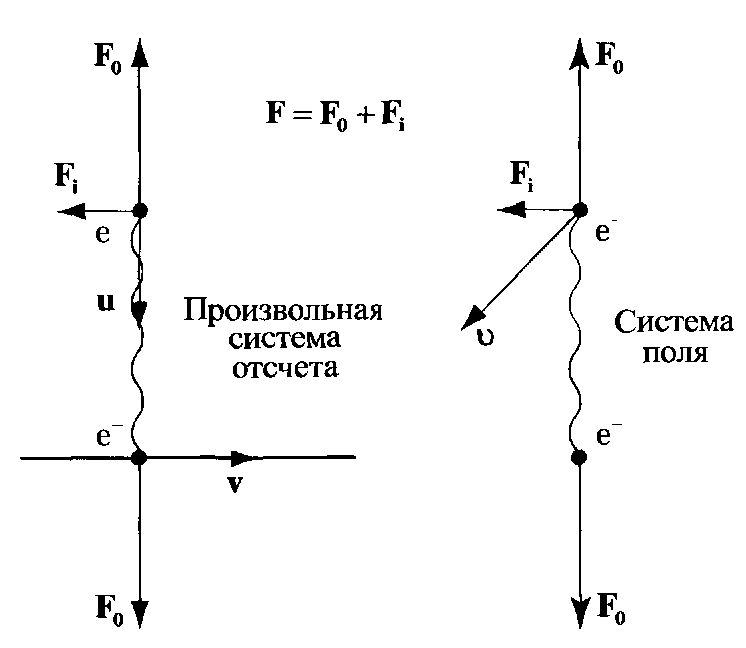Рисунок 4.16.2. При взаимоперпендикулярном движении частиц наличие сил инерции исключить невозможно. В этом случае инерциальной системы отсчета не существует в принципе.

правка к электростатической силе uv/с2 равна нулю и уже не компенсирует магнитную силу! Поэтому величина силы в этом случае будет отличаться от электростатической на такую же величину:

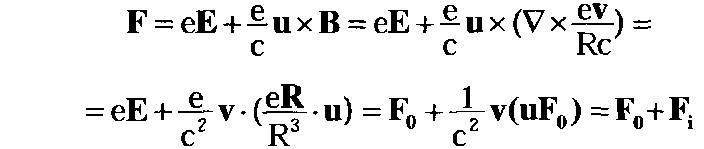(4.16.15)

В этом и состоит суть решения проблемы относительности в полевой физике. Соотношения между относительными величинами, характеризующими динамику системы, остаются неизменными независимо от того, в какой системе отсчета они записаны. Эти взаимосвязи являются едиными для любой системы отсчета, в том числе неинерциальной. Однако внешний вид уравнения движения в каждой системе отсчета свой. В зависимости от характера движения выбранной системы отсчета в ней возникают одни силы инерции и пропадают другие. Но связь между относительными динамическими характеристиками физической системы остается неизменной.

295

Пример со взаимноперпендикулярным движением частиц создал много проблем в классической электродинамике. Это связано с тем, что он представляет собой случай двухкомпонентной полевой среды, в которой каждая из компонент (частиц) движется неодинаково. В этих условиях в принципе не существует инерциальной системы отсчета в классическом смысле этого слова. В какую бы систему мы не перешли, всегда будет присутствовать та или иная дополнительная сила, похожая на полученную нами выше. Она представляет собой не что иное, как полевую силу инерции:

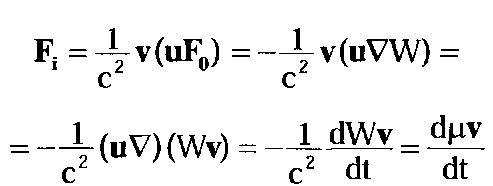(4.16.16)

А наличие силы инерции в инерциальной системе отсчета является абсурдным как с точки зрения классической, так и современной физики. В этих концепциях отсутствуют представления о силах инерции второго рода, связанных не с неравномерным движением, а с переменным характером массы. Поэтому в данном примере происходит нарушение равенства силы действия и противодействия, не сохраняется импульс. Решение современной физики также носит формальный характер и состоит в наделении импульсом самого поля. Это, вообще говоря, некорректно, потому что импульс — характеристика движения материальных частиц, а не полевой среды. Но как несложно видеть, изменение такого импульса поля Р (с обратным знаком) как раз и представляет собой неучтенную полевую силу инерции, связанную с движением источника локального поля: