Следуя логике классической силы Лоренца, мы должны описать движение второй частицы в поле произвольно движущейся первой частицы. Перенося слагаемое, описывающее влияние частицы-источника, в правую часть полевого уравнения движения (выражение 4.13.10), мы получаем:

A^ = vw+A^ = w + |^j+X(uV)(Wv)

(4.14.1)

Раскрывая полную производную по времени, мы учли то обстоятельство, что пространственная производная связана с движением второй частицы — частицы регистрации. Последнее слагаемое в свою очередь можно представить в виде:

(uV) (Wv) = v(uVW) = u х (v х VW) + (uv) VW (4.14.2)

В результате полевое уравнение движения, аналогичное классической силе Лоренца, принимает вид:

i^=Vw(.+^)+|^+iu><(v><vw)

(4.14.3)

Теперь нам осталось только проставить привычные обозначения. Прежде всего, массы. Как и ранее, мы считаем, что имеет место глобальное взаимодействие Wg = const, которое обуславливает постоянную классическую массу частицы регистрации:

279

m =--f (4.14.4)

с

А также есть локальное электромагнитное взаимодействие W|, влияние которого и описывает сила Лоренца. Оно обуславливает хорошо знакомую нам из первой главы полевую добавку к классической массе:

W

Ц =--г (4Л4.5)

с

Как и следовало ожидать, полевое уравнение движения описывает как «полевые» силы инерции, которым уделялось внимание в первой главе, так и обычные классические силы инерции. Пусть для простоты локальное взаимодействие пока вообще отсутствует, то есть Wj = 0. Тогда с учетом Wg = const движение частицы в произвольной системе отсчета принимает вид:

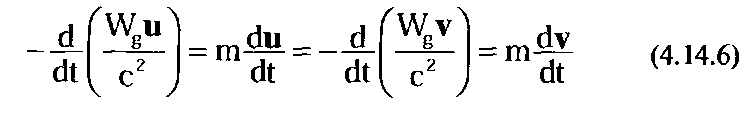Таким образом, если мы рассматриваем движение в системе отсчета, связанной с центром нашей Галактики, — основным источником глобального поля, или другими словами, в системе неподвижных звезд, то никаких сил инерции не возникает, так как v = 0! В этом и состоит суть динамического принципа инерции. При отсутствии внешних сил тело сохраняет состояние равномерного прямолинейного движения, но не по отношению к пространству как таковому или к инерциальной системе отсчета, а по отношению к основному скоплению гравитационных источников в Галактике, которые обуславливают его массу!