Предыдущая Следующая
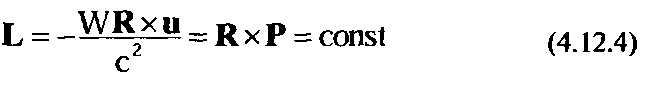 Несложно получить выражение для момента импульса в классическом приближении. Используя как и прежде значение функции полевой связи в виде W = Wg+ W,, мы получаем
271
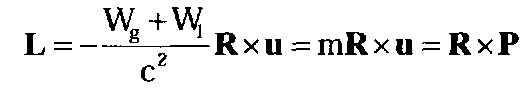 (4.12.5)
известное выражение для момента импульса.
В релятивистском приближении:
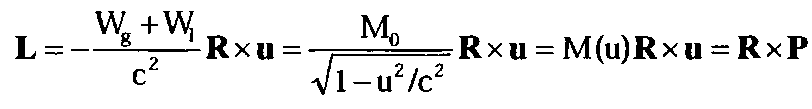 (4.12.6)
Гораздо интереснее становится роль закона сохранения момента импульса в чистом полевом случае без учета глобального взаимодействия
и постоянной составляющей массы. Если считать W = k/R, где
k = const, то закон сохранения импульса принимает вид:
где eR — единичный вектор в направлении R. Это выражение означает, что в процессе такого движения остается неизменной тангенциальная компонента скорости частицы ит. В отличие от классического движения, при котором в центральном поле остается неизменной «заметаемая» объектом площадь RuT/ 2, в случае чистого полевого движения этот закон трансформируется в закон сохранения скорости вращения
ит ! Но это уже совсем иная механика. И о ней мы подробно поговорим в следующей главе.
4.13. Взаимодействие произвольно движущихся зарядов
Мы постепенно подобрались к концу главы о релятивистском движении. Термин «релятивистское» мы использовали потому, что этот класс движения оказался полностью эквивалентен механике специальной теории относительности. А значит, полевая физика фактически позволяет заменить собой эту теорию, устранив всю связанную с ней мистику и иные проблемы. Однако чтобы полностью оправдать использование данного термина, нам осталось окончательно разобраться с проблемой относительного движения. Или другими словами, решить задачу о взаимодействии произвольно движущихся зарядов.
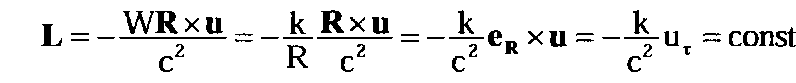 (4.12.7)
272
Эквивалентность этих двух задач возникает по следующим причинам. Пусть две заряженные частицы движутся произвольным образом в некой произвольной системе отсчета. Мы можем исследовать их движение именно в этой системе отсчета, и тогда нам придется учитывать все дополнительные поправки к силе, связанные с движением источника. Но мы можем также перейти в систему отсчета, связанную с одной из частиц, то есть в систему поля, в которой источник покоится, и присутствует только статическая сила. А уже потом вернуться в начальную систему отсчета, где движение частиц произвольно. В классической физике для этого использовались очевидные преобразования Галилея. В современной физике все оказалось гораздо сложнее.
Предыдущая Следующая
|