Все подобные усилия способны привести только к открытию тех явлений и законов, которые оказались уже заложенными в аксиомы данной геометрии или математической доктрины. В итоге этот путь оказывается замкнутым кругом, по которому ученые могут ходить годами или даже веками, теряя всякую надежду найти выход. И одним из наиболее ярких примеров подобного блуждания по замкнутому кругу является программа построения единой теории поля в рамках геометризации всех уравнений физики, провозглашенная еще во времена Эйнштейна. Все подобные попытки уже давно стали оторванными от реальности и свелись к элементарному перебору бесконечного множества комбинаций абстрактных математических величин.

Полевая физика позволяет по-иному посмотреть на математику. И существенно изменить приоритеты в научном мировоззрении и методологии. Только так можно разорвать замкнутый круг, не позволяющий достичь новых знаний и более глубокого понимания устройства нашего Мира.

270

4.12. Вращение и момент импульса

Сделав очередное философское отступление, нам следует вернуться к сугубо практическим вопросам и упомянуть еще одну производную характеристику движения, известную как момент импульса. Представления об этой величине возникают благодаря возможности получить еще один общий интеграл полевого уравнения движения:

Это становится возможным благодаря векторному умножению данного уравнения на расстояние между частицами R:

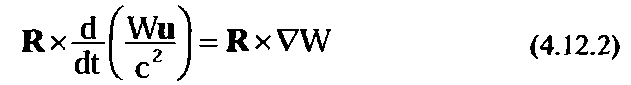Сразу же следует отметить, что правая часть этого уравнения равна нулю. Вид функции W в полевой физике представляет собой выражение W = const /R, а градиент этой величины сонаправлен с вектором R . В терминах классической физики это означает, что мы имеем дело с центральным полем.

Левая часть написанного выше уравнения может быть преобразована с помощью формулы производной произведения:

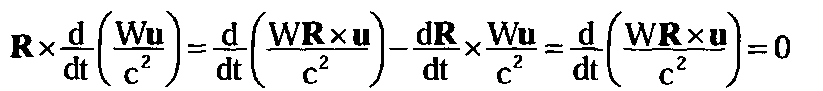(4.12.3)

Второе слагаемое в этом выражении также равно нулю, так как

dR/dt = и . В результате мы получаем, что в процессе движения частиц в согласии с полевым уравнением движения остается неизменной величина, которую мы и будем называть моментом импульса.

Момент импульса является физической величиной, характеризующей движение частиц в полевой среде. Он остается неизменным в процессе движения и определяется выражением: