М0. Так, при и = 0:

E|u=o =(Wg+W,)|u=0 = (-Mc2)|u=0 =-М0с2 = const (4.6.10)

или

М0 =-±(Щ+Щ)\и__0 =m-_LWl|u=0 (4.6.11)

Во многих случаях подобная масса покоя с хорошей точностью соответствует использованной выше классической массе т, учитывая что

Wg » W,, а значит, и та и другая массы определяются в основном глобальным взаимодействием. Хотя так бывает не всегда, и как мы увидим чуть ниже, это обстоятельство имеет очень большое значение.

Суть состоит в том, что классическая масса частицы, определяемая величиной Wg, в данной области космоса всегда имеет одно и то же значение. Она не зависит ни от характера движения частицы, ни от конкретного типа локального поля. Масса покоя частицы, наоборот, хотя и остается постоянной в процессе одного отдельно взятого движения, но зависит от величины локального поля W, в точке покоя частицы U = 0, соответствующей именно этому движению. А значит, одна и та же частица в зависимости от начальных условий может иметь совершенно разную массу покоя, подобно тому, как она может иметь совершенно разную полную энергию в процессе различных движений!

Таким образом, в отличие от классической массы масса покоя характеризует не саму частицу, а только начальные условия движения, в котором частица участвует в данный момент. А значит использование массы покоя, как однозначного идентификатора частицы, не проходит даже в обычных земных условиях! Несколькими разделами ниже мы подробнее поговорим о том, как эта причина приводит к иллюзии возникновения целых серий элементарных «частиц», очень схожих по свойствам и различающихся в основном только массами покоя.

Но вернемся к релятивистскому выражению для энергии. В результате введения массы покоя оно приобретает вид:

250

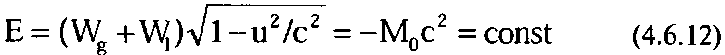или

]VLc2

, + = -W_ = const (4.6.13)

Vl-u2/c2

Релятивистский закон сохранения энергии можно оставить и в таком виде. А можно еще слегка преобразовать, выделив кинетическую энергию путем прибавления к обеим частям уравнения величины Е = —М0с2 и вводя эффективную энергию Е':

E'=E-Wg= ^ -M0c2+V^ = const (4.6.14) Vl-u2/c2

Релятивистский случай также допускает разделение энергии на кинетическую и потенциальную. Только в отличие от классического случая кинетическая энергия равна: