Еще один простой пример, который я называю множеством Безиковича, рассматривается в разделе НЕЛАКУН АРНЫЕ ФРАКТАЛЫ, 3.

Пусть р (х) — некоторая неубывающая функция от х е [0, 1]. Если максимальные открытые интервалы, в которых значение \х постоянно, составляют в сумме дополнение замкнутого множества 5, то мы говорим, что множество 5 является опорным для с1р(х). Преобразование Фурье-Стилтьеса функции р имеет вид

РАЗМЕРНОСТЬ ФУРЬЕ И ЭВРИСТИКА

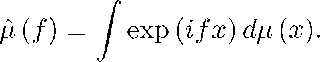39 о Математическое приложение и дополнения

511

Самые гладкие функции р дают наивысшую возможную скорость уменьшения Д. Обозначим через Dp наибольшее вещественное число, при котором по меньшей мере одна функция р (х) с носителем S удовлетворяет равенству

ß(f)=o{\f\-DF/2+e) присю для всех £> О, но ни одна р (х) не удовлетворяет

р (/) = о (\f\~DF^2~e) при / —> со для некоторых е > 0.

Выражение «а = о (Ь) при / —> сю» означает здесь, что lim (а/Ъ) =

= 0. Когда множество S заполняет весь интервал [0, 1], величина Dp бесконечна. И напротив, когда S — одна-единственная точка, Dp = 0. Интересно, что, когда S представляет собой множество нулевой меры Лебега, величина Dp конечна и не превышает размерности Хаусдорфа-Безиковича D этого множества. Неравенство Dp ^ D показывает, что фрактальные и гармонические свойства фрактального множества связаны между собой, но не обязательно совпадают.

Для доказательства того, что эти размерности могут различаться, предположим, что S — это множество на прямой, причем его размерность D равна Dp. Если рассматривать S как множество на плоскости, то размерность D не изменится, a Dp обратится в нуль.

Определение. В качестве удобного способа обобщения некоторых гармонических свойств S, предлагаю назвать величину Dp размерностью Фурье множества S.

Множества Сейлема. Равенство Dp = D описывает целую категорию множеств, называемых множествами единственности, или множествами Сейлема (см. [255, 248]).

Эмпирическое правило и эвристика. Интересующие нас в прецедентных исследованиях фракталы оказываются, как правило, множествами Сейлема. Поскольку величина Dp во многих случаях легко определяется из экспериментальных данных, можно использовать ее для оценки D.