470

Разное о XI

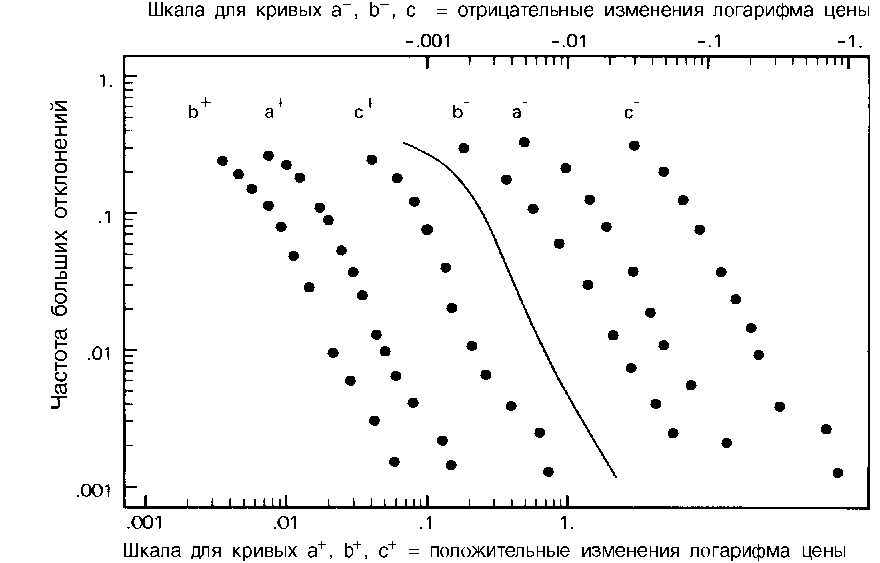Скопируйте эту иллюстрацию на кальку и подвигайте ее по горизонтали. Вы обнаружите, что теоретическая кривая совпадает с любой из эмпирических кривых с точностью до незначительных отклонений общей формы. Именно такой результат и постулируется в моем скей-линговом принципе!

Отклонения вызваны, по большей части, небольшой асимметрией в распределении. Согласно этому важному наблюдению, должны существовать асимметричные варианты устойчивого распределения.

На графике отображены следующие серии данных (положительные и отрицательные значения X рассматривались в каждом случае отдельно):

а) X = 1п Z (Ь +1 день) — \nZit), где 2 — ежедневный курс на момент закрытия Нью-Йоркской хлопковой биржи, 1900-1905 гг. (Данные предоставлены Министерством сельского хозяйства США.)

б) X = 1п 2 (£ + 1 день) — \nZ (Ь), где 2 — индекс ежедневных цен на хлопок на различных биржах США на момент закрытия, 1944-1958 гг. (Данные предоставлены Хендриком С. Хаутаккером.)

в) X = 1п 2 (£ + 1 месяц) — 1пИ (£), где 2 — курс на момент закрытия Нью-Йоркской хлопковой биржи 15 числа каждого месяца, 1880 1940 гг. (Данные предоставлены Министерством сельского хозяйства США.)

38 о МАСШТАБНАЯ ИНВАРИАНТНОСТЬ И СТЕПЕННЫЕ ЗАКОНЫ БЕЗ ГЕОМЕТРИИ

Если когда-либо будут написаны монографии или даже учебники по фракталам, то их авторы, вероятно, поместят главы, посвященные рассмотрению случайных геометрических фигур (весьма деликатный в математическом смысле предмет), после более простых глав, описывающих случайные функции, а начинаться эти книги будут, конечно же, со случайных величин. В настоящем эссе мы поступили иначе, сразу окунувшись с головой в наиболее сложную тему, поскольку тема эта представляет наибольший интерес и дает наибольший простор для развития геометрической интуиции.

Ближайшие родственники фракталов — гиперболические распределения вероятностей. В предыдущих главах мы встречали немало примеров их применения, начиная с гиперболических функций №(Г/ > и). Однако многое осталось недосказанным. Эта глава начинается с общих замечаний о предмете, а затем мы рассмотрим некоторые лингвистические и экономические феномены, относительно которых имеются многочисленные и убедительные эмпирические свидетельства, очень хорошо описываемые гиперболическими законами. Рассуждения в обоих случаях одинаковы и представляют масштабную инвариантность и размерность подобия в совершенно «развоплощенном» виде.