Пока остаточные кварталы имеют размерность И > 1, их перес чение произвольной прямой представляет собой пыль Леви с размерн стью £) — 1. Если же И < 1, то пересечение почти наверное являет! пустым множеством. Этот вывод, однако, не представляется очевидны так как на рисунке невозможно отобразить сколько-нибудь поздний эт; построения.

В главе 33 имеется более удачная иллюстрация. В случае, когда вычитаемые из плоскости тремы представляют собой случайным образом расположенные диски случайного размера, как показано на рис. 424-421, пересечения трема-фракталов с прямыми суть не что иное, как пыль Леви. ■

Рис. 399 и 400. ДЬЯВОЛЬСКИЕ ЛЕСТНИЦЫ ПОЛЯ ЛЕВИ (РАЗМЕРНОСТЬ £> = 1; РАЗМЕРНОСТИ МНОЖЕСТВ АБСЦИСС СТУПЕНЕЙ РАВНЫ, СООТВЕТСТВЕННО, £> = 9/10, £> = 3/10

И £> = 0, 6309)

Эти графики представляют собой рандомизированные аналоги функции Кантора (иначе — чертовой лестницы) с рис. 125. Размерность наибольшей из этих лестниц Леви равна размерности канторова оригинала; размерности двух оставшихся лестниц либо намного меньше, либо намного больше.

Для того чтобы построить лестницу Леви, рассмотрим абсциссу как функцию от ординаты. На первом этапе будем увеличивать

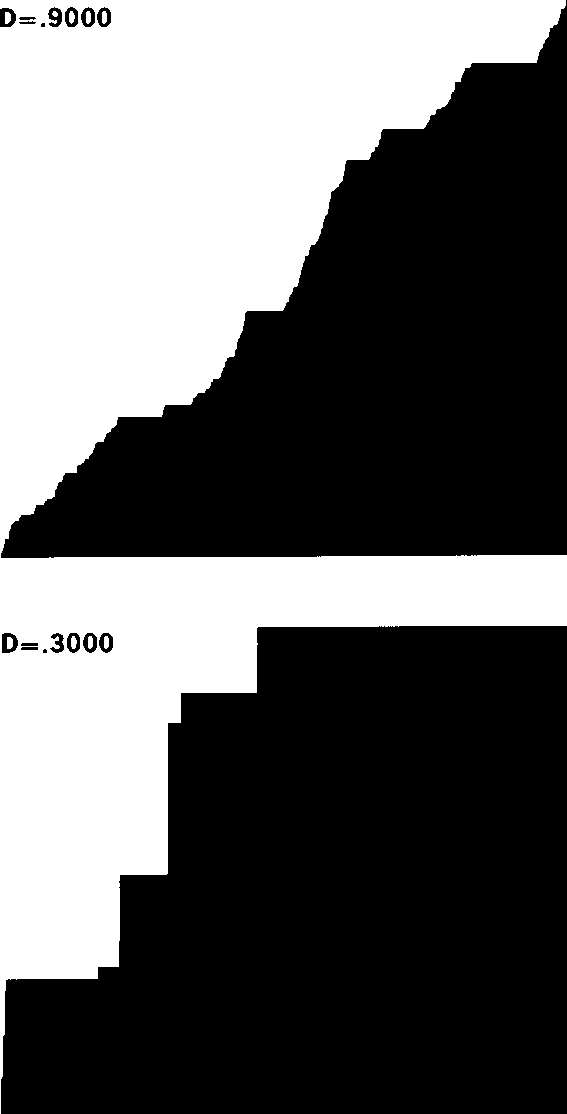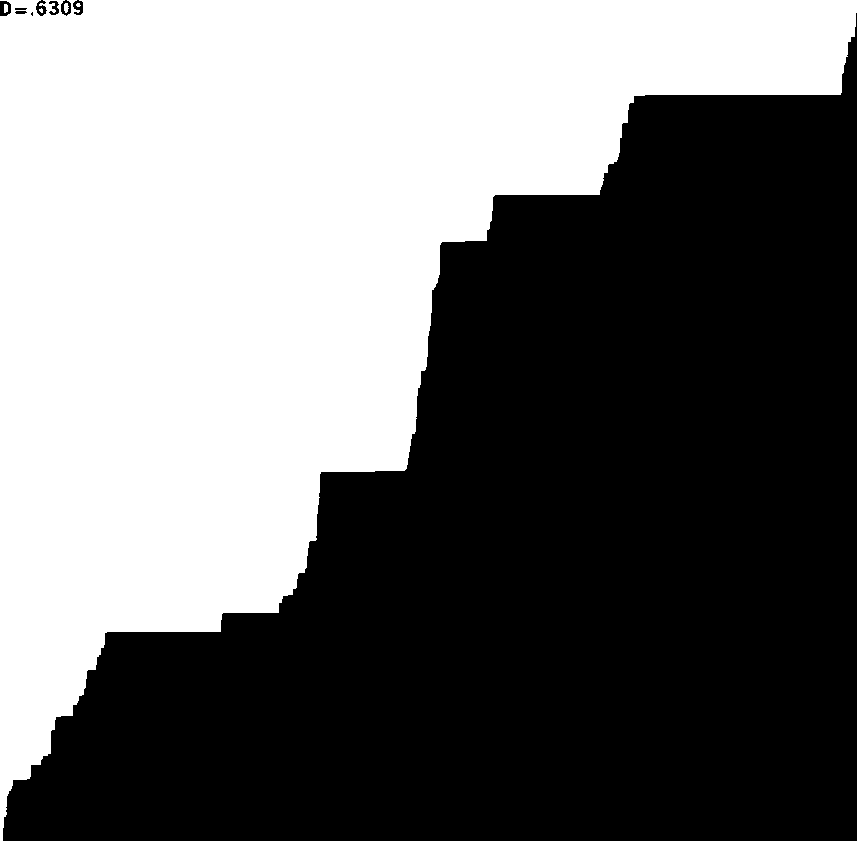абсциссу на некоторую случайную величину согласно распределению Рг(АХ > и) = и~ при всяком увеличении ординаты на величину Ау (в наших примерах Ау = 0,002). На втором этапе масштабируем абсциссу так, чтобы лестница заканчивалась в точке (1, 1). Количество ступеней в маленькой лестнице с И = 0,3 кажется меньше из-за чрезвычайно сильной кластеризации абсцисс ступеней.

32 о СУБОРДИНАЦИЯ. ПРОСТРАНСТВЕННАЯ ПЫЛЬ ЛЕВИ. УПОРЯДОЧЕННЫЕ ГАЛАКТИКИ

Центральной темой этой и следующей глав являются скопления галактик (эту тему мы уже затрагивали в главах 9, 22 и 23). Пользуясь известными методами, мы обобщим пылевидные множества из предыдущей главы на плоскость и пространство. В настоящей главе мы будем в основном заниматься пространственной пылью Леви. Следуя Бохнеру, мы введем эти фракталы посредством «обработки» броуновского движения по методу «субординации». Вдобавок к пыли Леви мы познакомимся с полетом Леви, представляющим собой нестандартное случайное блуждание. Начинается глава с неформального предисловия, посвященного кластерам случайного блуждания. Далее, путем обобщения на неслучайные структуры объясняется и обосновывается метод субординации. Утверждения, сделанные в предисловии, обосновываются в последнем разделе.