< Наиболее широко распространенный критерий масштабной инвариантности основан на спектрах. Шум можно считать спектрально масштабно-инвариантным, если его измеренная спектральная плотность на частоте / имеет вид 1//^, где /3 — некоторый положительный показатель. В случае, когда величина [3 настолько близка к 1, что становится возможным заменить 1//^ на 1//, мы получаем так называемый «1//-шум». ►

27 о Стоки рек. Масштабно-инвариантные сети и шумы 357

Многие масштабно-инвариантные шумы находят в своих областях весьма интересные применения, а объединяет все эти шумы то, что их можно встретить буквально повсюду. ■

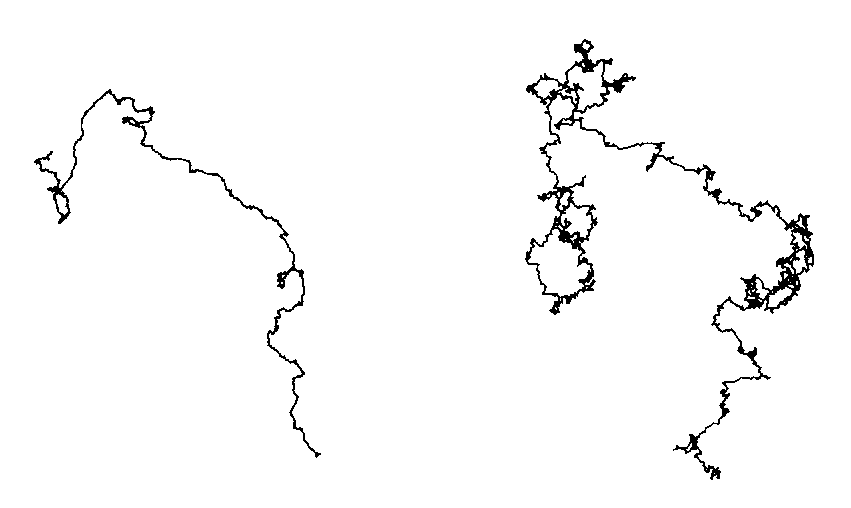
Рис. 357. ДРОБНЫЕ БРОУНОВСКИЕ СЛЕДЫ (РАЗМЕРНОСТИ D ~ 1,1111 И D ~ 1,4285)

На рисунке слева представлен пример статистически самоподобной фрактальной кривой с размерностью D = 1/0,9000 ~ 1,1111. Ее координатные функции — независимые дробные броуновские функции с показателем Н = 0, 9000, которым и обусловлено возникновение на Ниле эффекта Иосифа. Того обстоятельства, что Н близок к 1, оказывается недостаточно для предотвращения самопересечений, однако оно весьма осложняет им существование, побуждая «тренд» кривой к персистент-ности в любом направлении, какое он уже избрал. Представляя сложные кривые как наложения друг на друга больших, средних и малых сверток, можно сказать, что в случае высокой персистентности и близости размерности к единице малые свертки едва различимы.

Для рисунка справа мы воспользовались той же компьютерной программой, что и для рисунка слева, изменив лишь размерность D (теперь она равна D ~ 1/0,7000 ~ 1,4285). Псевдослучайная затравка не изменилась, поэтому общая форма линии остается узнаваемой. Однако увеличение D приводит к росту относительной значимости малых сверток, а также — до некоторой степени — и средних. Становятся отчетливо видны ранее невидимые детали.

28 о РЕЛЬЕФ И БЕРЕГОВЫЕ ЛИНИИ

В этой главе, главными героями которой являются абсолютно искусственные изображения, имитирующие карты и фотографии гор и островов, мы предполагаем показать, что с помощью должным образом подобранных фрактальных поверхностей, определяемых броуновской случайностью, можно очень легко моделировать в первом приближении любые горы (например, Альпы). Кроме того, мы наконец познакомимся с разумной моделью естественных структур, с которых начиналось настоящее эссе, но которые до сих пор не давались нам в руки, — я говорю о береговых линиях.