СЕПАРАТОР КАК ФРАКТАЛЬНАЯ КРИВАЯ; ПОКАЗАТЕЛЬ ФЕЙГЕНБАУМА 6 КАК СЛЕДСТВИЕ

Я предполагаю, < исходя из «перенормировочных» соображений ►, что чем дальше находятся атомы от затравки своей молекулы, тем более идентичными становятся их формы.

Следствие: граница каждой молекулы локально самоподобна. Так как она не является гладкой в малом масштабе, мы можем считать ее фрактальной кривой.

Это локальное самоподобие позволяет обобщить одно свойство бифуркации Мирберга, о котором сообщают Гроссман и Томэ [179], а также Фейгенбаум [142]. Длины отрезков, отсекаемых все уменьшающимися отростками на вещественной оси Лид, образуют убывающую геометрическую прогрессию с коэффициентом 5 = 4, 66920 ... (см. [83]). Первоначально считалось, что существование коэффициента 5 обусловлено особенностями аналитического метода. Рассмотренный в новом свете показатель 5 оказывается связан с более широким свойством фрактального скейлинга.

Каждая бифуркация из т > 2 ветвей вводит дополнительный базисный коэффициент.

Рис. 264. САМОКВАДРИРУЕМЫЕ ФРАКТАЛЬНЫЕ КРИВЫЕ ПРИ ВЕЩЕСТВЕННОМ ЗНАЧЕНИИ А

Фигуры на рисунках 264-273 публикуются впервые (за некоторыми исключениями, использованными мною в [398]).

Слева представлены наибольшие ограниченные самоквадрируемые области при различных значениях Л (а именно, 1,0; 1,5; 2,0; 2, 5 и 3,0). Черная фигура в центре охватывает интервал [0, 1].

А = 1: двустворчатая раковина.

А = 3: дракон Сан-Марко. Своего рода безудержная математическая экстраполяция очертаний венецианской базилики на фоне неба вместе с ее отражением в затопленной пьяцце: я окрестил эту кривую драконом Сан-Марко.

Справа помещена кривая при А = 3, 3260680. Это значение А является ядерным (согласно определению на с. 262) и соответствует периоду IV = 2. Кривая развернута на 90°, иначе она не входила в отведенные для иллюстрации рамки.

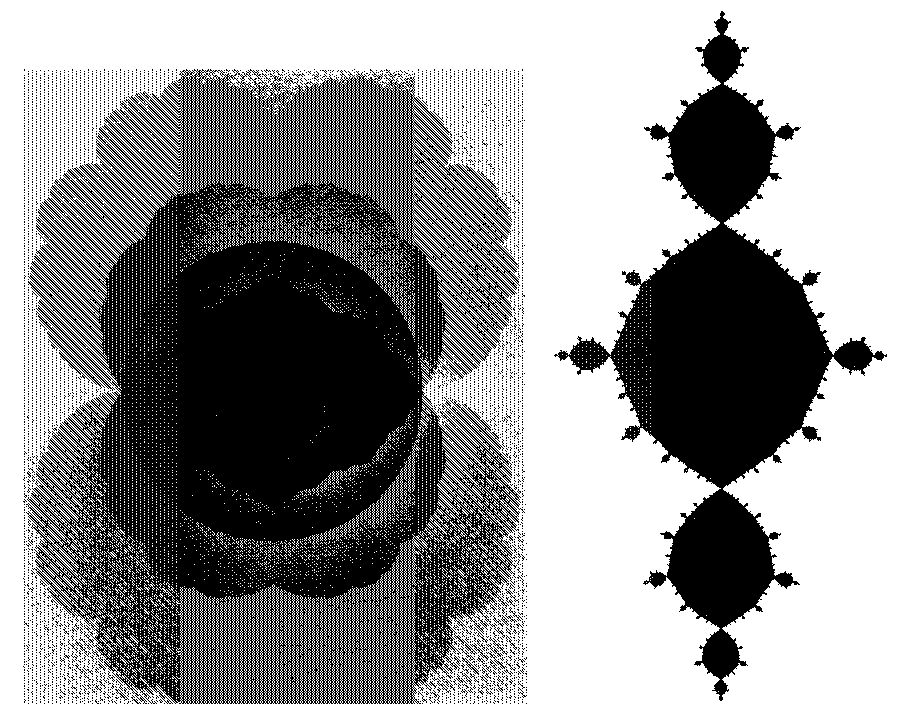Рис. 266. ОБОБЩЕНИЕ САМОКВАДРИРУЕМЫХ ФРАКТАЛЬНЫХ КРИВЫХ ПРИ ВЕЩЕСТВЕННЫХ А

Изображенная на рисунке «драпировка» была построена в памяти компьютера с помощью процесса, который сводится к отсечению от исходного куба всех точек, итерации которых при отображении г —> \х (1 — £) уходят в бесконечность. Параметр Л — вещественное число, изменяющееся в интервале от 1 до 4. Ось Л расположена вертикально, а координаты х и у образуют комплексное число г = х + гу.