13 о Острова, кластеры и перколяция

181

Предостережение: не всякий массовый показатель является размерностью. Составная величина <2 представляет собой весьма важную характеристику. А так как это массовый показатель, возникает искушение назвать его размерностью, однако это искушение ничем не обосновано. При слиянии различных кластеров с одинаковой размерностью 1?с, но разными Л, £)с не изменяется, поскольку размерность — это не свойство совокупности различных множеств, но свойство каждого отдельного множества. И I?, и £)с являются фрактальными размерностями, а <Э — нет.

Обобщая, можно сказать, что во многих областях физики известны соотношения вида (М (В,)) ос В9, однако сама по себе эта формула еще не гарантирует того, что <2 непременно будет фрактальной размерностью. Называть же <2 эффективной размерностью, как предлагают некоторые авторы, все равно, что попусту сотрясать воздух, так как <2 не обладает ни одним из остальных свойств, характеризующих И как размерность (например, суммы или произведения размерностей И имеют смысл, которому нет аналогов в случае О). Более того, эти пустые слова оказываются источником возможных недоразумений.

РАССРЕДОТОЧЕННЫЕ КЛАСТЕРЫ, ПОЛУЧАЕМЫЕ ПРИ СТВОРАЖИВАНИИ

Существует еще два метода построения контактных кластеров. Первый основан на створаживании и применим в случае И < 2, второй использует кривые Пеано и пригоден для случая И = 2. Читатели, интересующиеся перколяцией, могут пропустить этот и следующий за ним разделы.

Начнем с замены построения Коха естественным обобщением кан-торова створаживания на плоскость. В качестве иллюстрации на нижеследующем рисунке представлены пять примеров генераторов, под которыми помещены последующие этапы построения:

В

Д

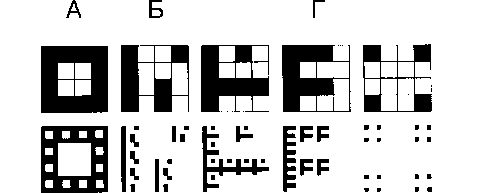Во всех этих случаях предельный фрактал имеет нулевую площадь и не содержит внутренних точек. Его топология зависит от формы генератора и может быть весьма разнообразной.

182

Масштабно-инвариантные фракталы о IV

В случае генератора А предтворог на каждом этапе построения представляет собой связное множество, а предельный фрактал оказывается кривой — примером может служить чрезвычайной важности конструкция (называемая ковром Серпинского), которую мы подробно рассмотрим в главе 14.