Из построения матриц Ь„ и Н„ и свойства ортогональности (6.1.1) мы получаем следующее свойство ортогональности:

170 _Фракталы и вейвлеты для сжатия изображений в действии

где Оля - это нулевая матрица размером п/2 х п/2 и * означаег транспонирование матрицы. Мы наложим на Ь„ (а, следова. тельно на коэффициенты с0,...,с^.1) следующее условие:

где \пп - единичная матрица размера п/2 х п/2. Условие (6.2.1) эквивалентно равенству

(6.2.2)

(Є.2.3) НХ=1„/2

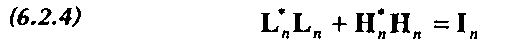Свойство (6.2.4) является аналогом свойства (5.7.10).

6. Вейвлеты Лобеши

171

шшт

. Вейвлет-преобразование

Вейвлет-преобразование может быть определено как дерево низкочастотных и высокочастотных фильтров, как показано на Рис. 6.3.1. Как и в случае с операторами усреднения и вычитания из главы 5, идея здесь достаточно проста. Низкочастотные фильтры {Ь„} уменьшают количество информации сигнала х. Высокочастотные фильтры {Н„} представляют недостающую информацию. На Рис. 6.3.1 показан пример вейвлет-преобразования элемента х из пространства К8. Напомним, что ЬЛ,НЛ:КЛ—^К"72, т.е. фильтры уменьшают размерность входного вектора наполовину. Вейвлет-преобразование - это элемент пространства К8 вида {ЬгЬД^х, НгЬД^х, Н4Ь8х, Н8х}. Таким образом, вейвлет-преобразование состоит из конечного взвешенного среднего ^ЬД^х и всех векторов деталей, сохраняемых на каждом шаге процесса преобраз