отражать размещение битов информации в исходном

бражении. Зато существует возможность распространи идею вейвлет-преобразования на последовательности бод^ шей размерности. Первый способ заключается в том, чтоб сначала преобразовывать строки изображения, а затем пре образовывать столбцы изображения с преобразованные строками. Это легко реализуется программно, так как однон то же одномерное преобразование может быть использовано для преобразования и столбцов, и строк изображения.

Чтобы увидеть, как работает эта процедура, рассмотрим дву, мерный аналог простой 4-элементной последовательности из раздела 5.3. Предположим, мы имеем изображение 4x4:

(5.8Л)

которое мы можем представить как функцию, заданную на единичном квадрате [0,1] х [0,1]:

(5.8.2)

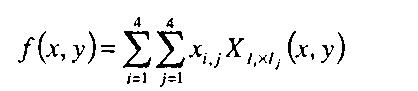Уравнение (5.8.2) - это двумерный аналог уравнения (5.3.1). Здесь

(5.8.3)

5» Простые вейвлеты

161

Подставив (5.8.3) в (5.8.2), мы получим

г

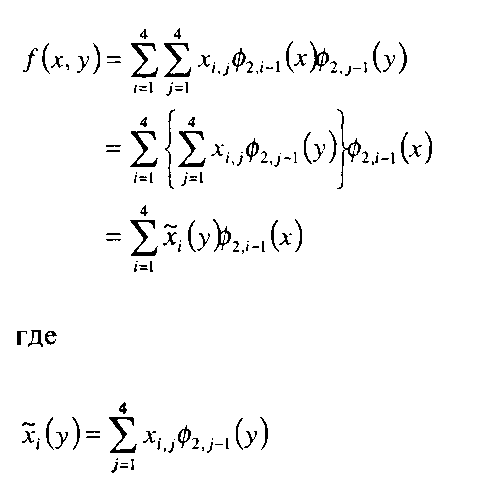Обратите внимание, что для каждого г = 1,...,4, уравнение (5.8.5) выглядит очень похожим на уравнение (5.3.4). Это означает, что мы можем применить одномерное вейвлет-преобразование так, как делали это раньше, для каждого 1,...,4 в (5.8.5). В результате мы получим новый набор уравнений для х,(у) * = 1>--->4, с коэффициентами, являющимися результатом вейвлет-преобразования последовательности *;(4}. Таким образом, мы получим следующее:

*|М = <оФо.оМ+<оУо^

для каждого I = 1,...,4. Это эквивалентно применению одномерного вейвлет-преобразования к каждой строке исходного изображения (5.8.1). Теперь подставим (5.8.6) обратно в (5.8.4) и переупорядочим члены, чтобы получить

162

Фракталы и вей влеты лля сжатия изображений в действии

Каждая из сумм в скобках в (5.8.7) опять очень похожа на уравнение (5.3.4), и поэтому одномерное вейвлет-преобразование может быть применено к каждому их этих выражений. Это эквивалентно применению одномерного вейвлет-преобразования к каждому столбцу исходного изображения (5.8.1).

Итак, один из способов получения двумерного вейвлет-преобразования изображения размером 2"х2п, заключается в том, чтобы сначала применить одномерное вейвлет-преобразование к каждой из Т строк, а затем применить одномерное вейвлет-преобразование к каждому из 2" столбцов. Это не единственный способ определения двумерного вейвлет-преобразование. Этот подход имеет очевидное преимущество в реализации, так как не требует никакой доработки уже имеющегося одномерного преобразования. Он очень эффективен для наших целей сжатия изображения.