Прежде чем мы продолжим этот процесс, зададим один напрашивающийся вопрос: как мы получаем коэффициенты равенства (5.6.2) из коэффициентов равенства (5.6.1)? Для этого мы используем ортогональность. Напомним, что каждая фп.\^ ортогональна каждой фп.\^ так же как и всем у/п-\^ и, аналогично, каждый вейвлет ортогонален другим

вейвлетам у/п-\Ук и всем масштабирующим функциям фп.ц- Напомним также, что каждая фп.\^ и каждый у/п-ц являются нормированными в силу тождеств (5.5.1) и (5.5.2). Чтобы воспользоваться этой ортогональностью и нормированностью, умножим обе части (5.6.2) на фп-\$) и проинтегрируем по I от О до 1. В результате получим

В силу ортогональности в правой части (5.6.4) остается только один член, а нормирование приводит к отсутствию коэффициента при а„.\^ Теперь подставим правую часть равенства (5.6.1) вместо Д*) в (5.6.4). Например, при у = 0 левая часть равенства (5.6.4) будет равна

0 Хч

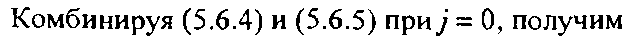154__Фракталы и вейвлеты для сжатия изображений в дейсп^

Квадратный корень в коэффициенте в (5.6.6) появляется счет нормирования. Если бы мы использовали ненормцр^ ванные базисные функции, то мы бы получили двухточечн среднее значение, рассмотренное в разделах «Усреднение детализация» и «Функции масштаба и вейвлет-функции». о* тальные коэффициенты ап.\,р ] = 1,...,2М вычисляются ан& логично. Таким образом,

(5.6.7)

Аналогично, используя свойства ортогональности и норми. рованности функций у/п-ц9 можно вычислить коэффициенты е!п-ц по следующей формуле

(5.6.8)

Еще раз напомним, что квадратный корень в выражении для коэффициента (5.6.8) появляется в результате нормирования. Без нормирования мы бы имели только разность выражений, полученную в разделах «Усреднение и детализация» и «Функции масштаба и вейвлет-функции».

Уравнения (5.6.7) и (5.6.8) удобно представить в виде одного матричного уравнения:

^5. Простые вейвлеты

155

Матрица в (5.6.9) - это квадратная матрица с 2п строками и 2п столбцами. Определим

где А„ и Б„ - матрицы размером 2я"1 х 2", и А„ можно рас-сматривать как оператор усреднения и Б„: К —»К - оператор разности. Введем также векторную запись