ляется:

Мы можем представить себе один шаг процесса вейвлет-преобразования, а именно шаг, состоящий в переходе от разрешения Vм к более низкому разрешению V*, как представление элемента е в базисе, который задается уравнением (5.4.2). Предположим, что gм е Vм первоначально был выражен как:

Тогда gk+\ может быть разложен по базису (5.4.2), например* таким образом:

5. Простые вей влеты

151

Коэффициенты {<4,о>... ,*4,2*-1} становятся частью вейвлет-преобразования. На следующем шаге этого процесса мы бы получили выражение

8* = акЖ.о + • • • + а^-А,*-! Е ук

Через {&-!,,} И

Нормирование

В дальнейшем нам будет удобно работать с нормированными масштабирующими функциями и вейвлетами. Определим норму вектора / в евклидовом пространстве следующим образом

Вектор и в евклидовом пространстве называется нормированным, если \\и\\ = 1. Нормированный вектор и может быть получен из любого ненулевого вектора / путем деления вектора/на его норму:

152 Фракталы и вейвлеты для сжатия изображений в действИц

для каждого у. Итак, для того, чтобы работать с нормиров^ ными масштабирующими функциями и вейвлетами, необх0 димо переопределить их. Для этой цели мы определим А как: ]

Будем называть вейвлеты, заданные равенством (5.5.2) (где у определяется равенством (5.3.6)) нормированными вейвлетами Хаара.

5.6. Вейвлет-преобразование

Предположим, что мы имеем последовательность, состоящую из 2п точек {х1,х2,.~,х п} для некоторого целого п > 0.

Мы можем отождествить эту последовательность со следующей функцией из Уп:

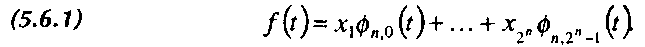Первым шагом вычисления вейвлет-преобразования последовательности {хх,хг,...,хгП} будет разложение Д/) по альтернативному базису пространства Уп вида (5.4.2), половину которого составляют вейвлеты:

(5.6.2) ап_10фп_10Ь)+... + «в.и2.-,.Л-..2-'.1 ^ +

Лп-х^п-иО (0 + • ■ ■ + ^-1.2-1-1^л-1.2-»-1 ^

Коэффициенты </дЧ>0,..., 2„_, _ при базисных вейвлет-

функциях составляют половину коэффициентов вейвлет преобразования, поэтому мы сохраним эти значения. Следующим шагом процесса преобразования является примене*

5. Простые вейвлеты

153

5)

Кб)

Таким образом, gn.\ это элемент уп'\ и поэтому может быть разложен по альтернативному базису, состоящему из масштабирующих функций фп.г^ и вейвлетов у/п-г^-