Предыдущая Следующая
7. Технологии вей влет-сжатия изображений
205
 І 7.2.13.
Сравнение PSNR и коэффиииента сжатия для алгоритма деиимаиии и алгоритма с нуль-деревом, использующего деиимаиию и 10 битовых плоскостей. Алгоритм с нуль-деревом дает лучшее сжатие, при этом внося меньшее значение PSNR. Используется изображение «Lena» 256 х 256 и 04-вейвлеты Лобеши
7.2.4. Скорость кодирования
Важное преимущество алгоритма с нуль-деревом, особенно по сравнению с фрактальным алгоритмом, это скорость кодирования. На Рис. 7.2.14 сравнивается время кодирования для алгоритма с нуль-деревом и базового алгоритма децимации. Сжатие достигается только за счет сокращения числа битовых плоскостей. Процесс децимации включает операцию сортировки, на которую приходится большая часть времени кодирования. Само вейвлет-преобразование изображения 256 X 256 занимает приблизительно 3 секунды. Алгоритм с нуль-деревом без децимации занимает всего секунду или две, прибавляемые ко времени преобразования. Это время включает время записи символов в файл. Время децимации увеличивается с увеличением процента сохраняемых коэффициентов. Для 1% сохраняемых коэффициентов (коэффициент сжатия 25:1) это время незначительно, и поэтому общее время кодирования приблизительно равно времени вейв-лет-преобразования, т.е. 3 секундам. Для 10% сохраняемых коэффициентов (коэффициент сжатия 2.5:1) время децима-
206
Фракталы и вейвлеты для сжатия изображений в деИ(
ции увеличивается до 15 секунд и составляет большую
общего времени кодирования, равного 18 секундам.
 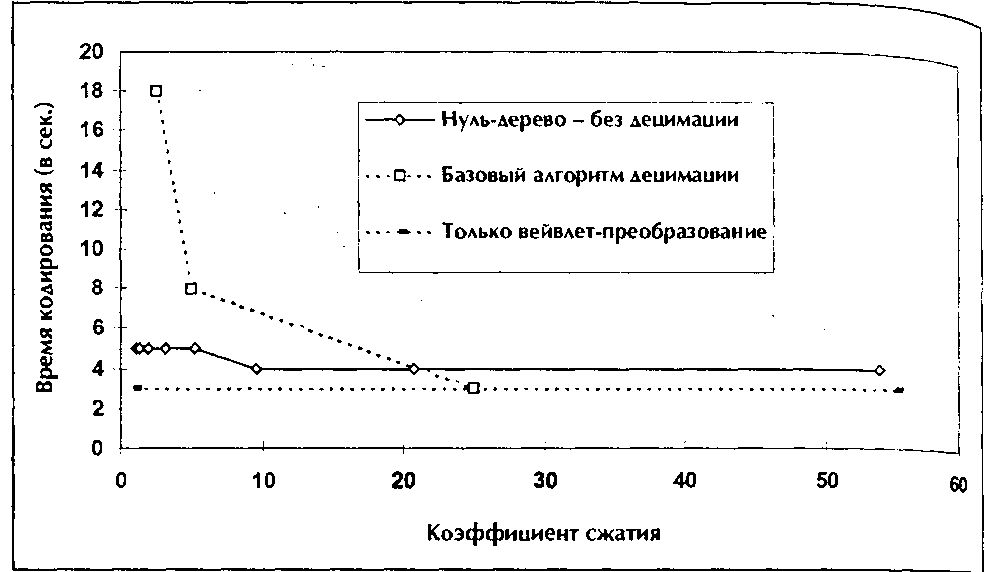 Рис. 7.2.14.
Зависимость времени кодирования от коэффициента сжатия лля кодирования с нуль-деревом без деиимаиии и базового алгоритма деиимаиии (процессор Pentium 200 МГи). Лецимания включает в себя операцию сортировки, на которую приходится большая часть времени кодирования для этого алгоритма
7.3. Смешанное фрактально-вейвлетное кодирование
Самоподобие при любом масштабе - это определяющее свойство фракталов. Вейвлеты с их способностью выделять информацию, зависящую от масштаба, являются естественным инструментом анализа фракталов. Поэтому неудивительно, что в последнее время исследовательская деятельность сконцентрировалась на комбинировании вейвлетных И фрактальных методов сжатия изображения. Дэвис [13, 14, 15] предложил подход, который использует элементы как фраК* тального, так и вейвлетного сжатия изображений и предо0' тавляет основу, которая связывает эти два подхода вместе-Асгари (Asgari) и др. [1] используют вейвлет-преобразование при построении неаффинного преобразования для схемЫ сжатия, основанной на системах итерируемых функций. Xе' берт и Саундарарян (Hebert, Soundararajan) [21] предлагав
Предыдущая Следующая
|