202

Рис 7.2 11. Прогрессивное декодирование изображения ~і.епа», которое было за-

кодировано с помошью алгоритма с нуль-деревом с 04-вейвлета^ Лобещи. Кажлое изображение злесь - это результат декодирован*1* соответствующей битовой плоскости с Рис. 7.2.9

рддВА^. Технологии вейвлет-сжатия изображений

203

7^

О

U)

-8--8-

Є

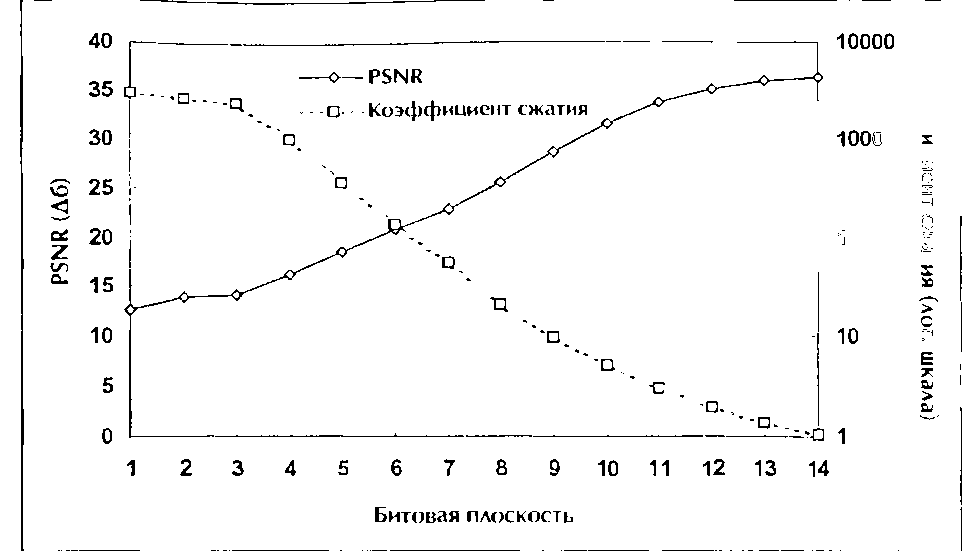
(а) Зависимость PSNR и коэффиииен п окзтия о битовой плоскости

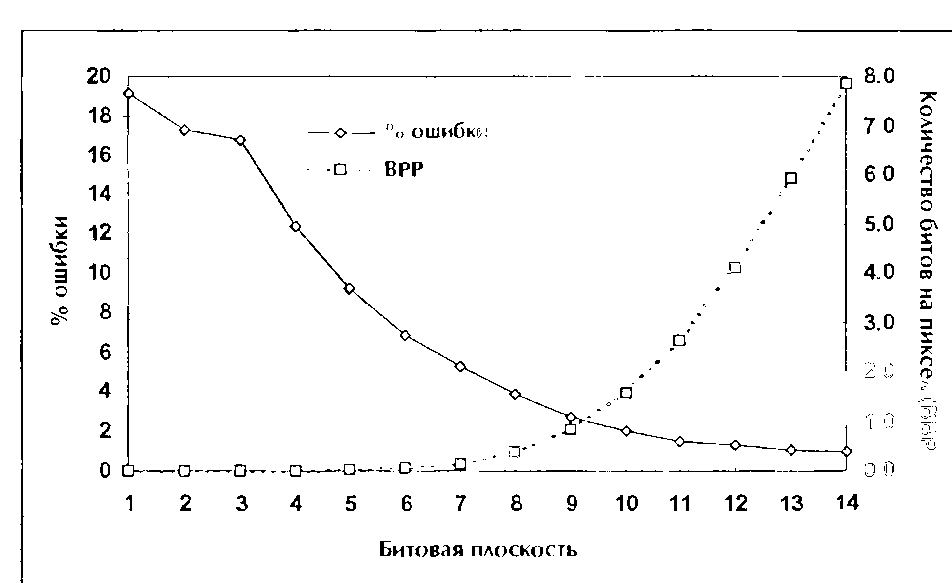(Ь) Зависимость пиксельной ошибки и количества битов на пиксел от битовой плоскости

Р«С 7.2.12.

Значения погрешностей и коэффициент} сжатия в зависимости от ко личества битовых плоскостей, Числа приведенные здесь, соответствуют изображению Lena размером 256x256 за коди рові иному с помошью алгоритма с нуль-деревом с использованием 04-веивлетов Лобеши, как показано на Рис 7 2 9 и 7 2 17

204 Фракталы и вейвлеты для сжатия изображений в действ

---—-----^Ju^

7.2.3. Где же сжатие?

На Рис. 7.2.12 также представлен фактический коэффицИеНт сжатия на каждом уровне декодирования битовых плоско стей. К сожалению, реализованный здесь алгоритм без эц тропийного кодирования символов при использовании всех битовых плоскостей не дает существенного сжатия. Но если мы исключим несколько последних битовых плоскостей, то при умеренном сжатии мы можем получить очень хорощее качество декодированного изображения. Например, на 1(Ц битовой плоскости декодированное изображение будет иметь 2.0% пиксельную ошибку (31.4 PSNR) с коэффициентом сжатия 5.16:1 (1.5 бита на пиксел). Поэтому количество битовых плоскостей включается в заголовочную информацию сохраненного закодированного изображения. Декодер может остановиться на желаемой битовой плоскости для достижения лучшего сжатия.

Существует и другой путь достижения лучшего сжатия. Мы можем скомбинировать метод децимации из предыдущих двух глав с алгоритмом нуль-дерева. Децимация применяется к вейвлет-коэффициентам перед кодированием с нуль-деревом. Если сохраняются все битовые плоскости, то результат получается примерно такой же, как для базового алгоритма децимации - и по ошибке декодированного изображения, и по коэффициенту сжатия. Например, если сохраняются 10% коэффициентов преобразования изображения «Lena» с помощью В4-вейвлетов Добеши, любой из алгоритмов дает коэффициент сжатия приблизительно равный 2.5:1 и 31-32 Дб PSNR. Мы можем улучшить коэффициент сжатия изображения, закодированного алгоритмом с нуль-деревом, за счет внесения небольшой ошибки в декодированное изображение путем сохранения только 10 битовых плоскостей. На Рис. 7.2.13 сравниваются базовый алгоритм децимации с алгоритмом с нуль-деревом, использующим децимацию и 10 битовых плоскостей. При сохранении 10 битовых плоскостей и 10% вейвлет-коэффициентов коэффициент сжатия составляет 7.35:1, a PSNR - 30.3 Дб.