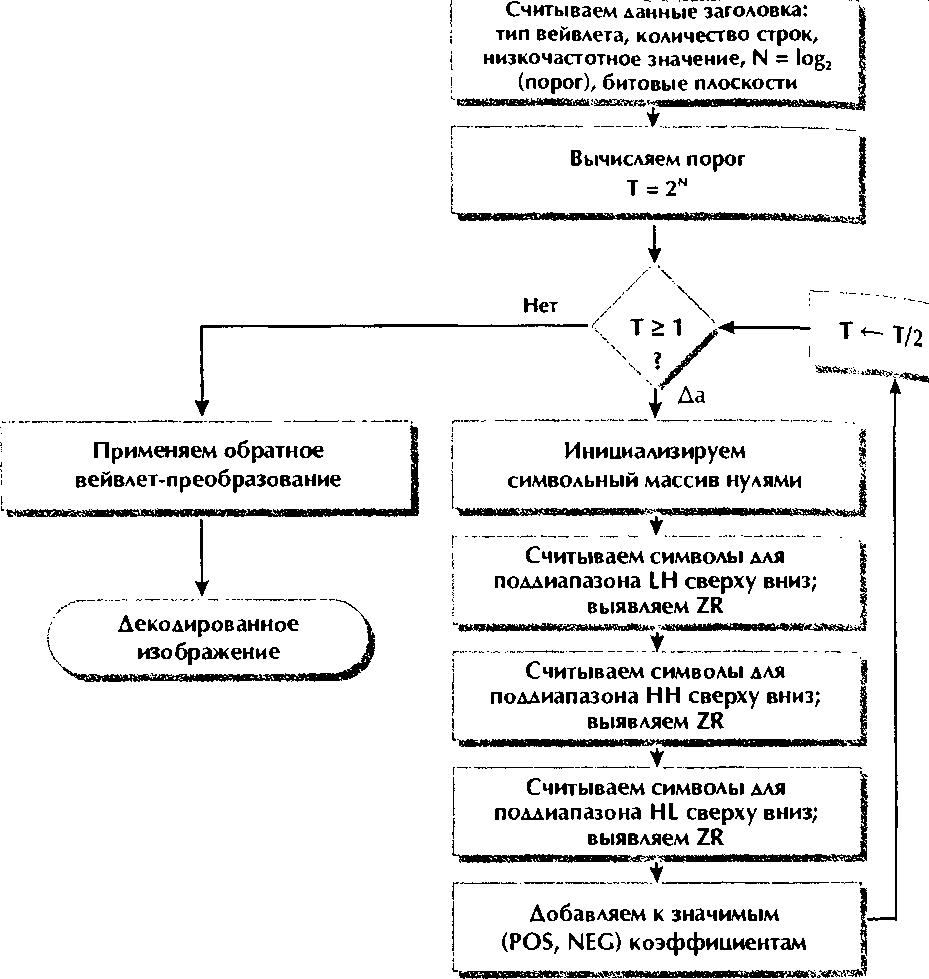Рис. 7.2.10.

Алгоритм леколирования с нуль-леревом

Значения коэффициентов вейвлет-преобразования содержатся в отдельном массиве. В начале процедуры декодирования этот массив вейвлет-преобразования инициализируется ну-лями. Коль скоро символьный массив был весь заполнен 0 данного значения порога, значения в массиве вейвлет преобразования обновляются путем добавления пороговое значения Т к каждому элементу массива, соответствуют^ символу РОБ, и вычитанием Т из каждого элемента массива соответствующего символу ИЕС Таким образом, значен коэффициентов вейвлет-преобразования реконструируй по их двоичным представлениям, причем вначале задейсТ^У ются наиболее значимые биты, а затем менее значимые

Технологии вейвлет-сжатия изображений

201

кодированное изображение получают путем применения обратного вейвлет-преобразования, после того как построена последняя битовая плоскость.

Именно такой порядок битовых плоскостей преобразованного изображения, от более значимых битовых плоскостей к менее значимым, дает декодирование с нуль-деревом, обладающее свойством прогрессивной передачи. Чтобы увидеть, сколько информации передается с каждой битовой плоскостью, рекомендуется применять обратное преобразование после построения каждой битовой плоскости. На Рис. 7.2.11 показан пример использования такой техники. Изображения на Рис. 7.2.11 были построены с использованием обратного 04-вейвлет-преобразования Добеши к битовым плоскостям, изображенным на Рис. 7.2.9.

На Рис. 7.2.12 показаны (а) РБМЯ и (Ь) пиксельная ошибка как функции количества битовых плоскостей для изображений, показанных на Рис. 7.2.11. Заметим, что когда все битовые плоскости объединены, описанный здесь алгоритм кодирования-декодирования с нуль-деревом гораздо ближе к алгоритмам без потерь. Дело в том, что алгоритм пытается закодировать все двоичное представление коэффициентов преобразования полностью, без отбрасывания какой-либо информации. Однако получается так, что небольшая ошибка квантования возникает из-за того, что вейвлет-коэффициенты являются значениями с плавающей точкой, а алгоритм кодирует только целую часть этих значений. Кроме того, возникает небольшая ошибка при применения операторов прямого и обратного вейвлет-преобразования. Это приводит к пиксельной ошибке (0.99%; 36.4 РБЫК), которая остается после декодирования, примененного ко всем битовым плоскостям.