6.7. Другие системы вейвлетов

Рассмотренные здесь вейвлеты Хаара и Добеши - это только маленький пример из огромного множества систем вейвлетов, используемых в приложениях обработки сигналов и изображений. Как уже говорилось, системы вейвлетов Хаара и Добеши обладают свойством компактности носителя, а также ортогональности. Таким образом, мае» штабирующие функции фк, и вейвлет-функции щ< удовлетворяют равенствам:

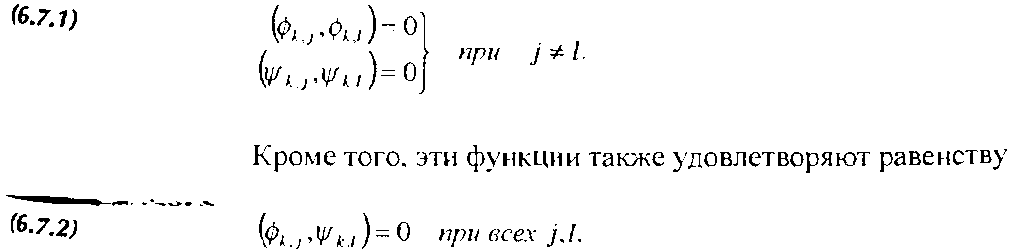180 Фракталы и вейвлеты для сжатия изображений в лействцц

Системы вейвлетов Добеши, кроме того, обладают свойств^ ми гладкости и исключения моментов.

Есть и другие свойства, которые могут быть полезны в сие темах вейвлетов. Одно из таких свойств - это симметрия, т е масштабирующие функции и вейвлет-функции симметрична относительно своих центров. Вейвлеты Хаара удовлетворяю? этому свойству, а вейвлеты Добеши - нет. Фактически вейв* леты Хаара - это единственные вейвлеты одновременно и симметричные, и ортогональные, и обладающие компактным носителем [12].

Поэтому, например, если нам нужны гладкие, симметричные вейвлеты с компактным носителем, мы должны отказаться от ортогональности. Многие из более новых систем вейвлетов, используемых в приложениях, не являются ортогональными в смысле удовлетворения условиям (6.7.1) - (6.7.2), но зато удовлетворяют некоторым более слабым свойствам ортогональности. Одно такое свойство - это полуортогональность [43]. Полуортогональные системы вейвлетов удовлетворяют равенству (6.7.2), но не удовлетворяют (6.7.1).

Другая слабая форма ортогональности - это биортогональность. Биортогональность относится к концепции ДВОЙСТВеННОСТИ. ПреДПОЛОЖИМ, ЧТО {Иь«2>..мИл} - это

множество неортогональных базисных функций. Мы можем представить функцию/в виде линейной комбинации этих базисных функций:

Отсутствие ортогональности делает более трудным определение коэффициентов я/. Однако существует другой базис и19и2,...9ип9 такой что

Функции и] обладают также свойством

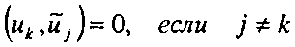6. Вейвлеты Добеши

181

Базис {мрМ2,...,мп} называется двойственным базисом, соответствующим {м1,М2,...,и„}. Биортогональные вейвлет-системы состоят из четырех множеств функций: базиса масштабирующих функций \!>кг]}, двойственного к нему базиса