Независимость природы протекания процесса от способа его наблюдения не означает единую видимость протекания процесса для всех наблюдателей. В разных системах отсчета описание протекания процесса может выглядеть по-разному, то есть описываться разными уравнениями с разным набором слагаемых.

Требование сохранения единого вида уравнений физики во всех инерциальных системах отсчета является искусственным. Инвариантным является только алгоритм составления уравнения движения, позволяющий написать правильную формулу в любой системе отсчета.

Физика накопила множество способов описания движения — своеобразных языков. Поэтому даже в рамках одной системы отсчета одно и то же движение может быть описано по-разному. Например, движение планеты по эллипсу в декартовых координатах (х,у) есть сумма квадратов:

64

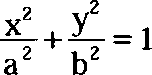(1.12.4)

где а и b — полуоси эллипса. А в полярных координатах (р,В) движение — обратный косинус:

это же

(1.12.5)

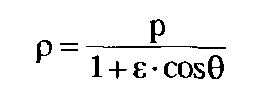где р и 8 — параметр и эксцентриситет эллипса. Форма записи законов движения разная, и важно лишь то, что две эти формулы описывают одну и ту же кривую! Это смысл выражений, который инвариантен.

В заключение этой темы следует отметить еще одно забавное обстоятельство. Согласно первому закону Ньютона всегда можно указать инерциальную систему отсчета, в которой объект движется без сил инерции. А мы случайно доказали, что нет!

Рассматривая движение частицы регистрации в поле частицы-источника, которая сама испытывает сложное движение относительно лаборатории, мы увидели следующее. В системе частицы-источника электрическая сила имеет простой вид, без инерционных добавок, зато в этой системе следует учитывать механические силы инерции. В лабораторной системе нет механической инерции, зато возникают полевые силы инерции. В некой промежуточной системе отсчета вообще будут присутствовать и одни силы инерции и другие. Несложно убедиться, что в этой задаче вообще нельзя так выбрать систему отсчета, чтобы избавиться от всех сил инерции сразу!

Почему это происходит? Потому что в нашем примере имеет место двухкомпонентное взаимодействие. Есть предпочтительная система отсчета для механики — лабораторная. И есть предпочтительная система для электродинамики — система частицы-источника. Модель инерциальной системы отсчета работает только тогда, когда есть одна предпочтительная система, или однокомпонентное взаимодействие. Или несколько предпочтительных систем отсчета совпадают друг с другом. Это частный случай, составляющий предмет классической механики.