где характерное время реакции системы X пропорционально массе:

Таким образом, масса тела оказывается тем больше, чем дольше время реакции этого тела на внешние воздействия и чем сложнее такому изменению произойти. А изменение скорости каждой частицы при их взаимодействии происходит тем сложнее и дольше, чем сильнее их полевая связь, то есть, чем больше абсолютное значение потенциала или чем ближе частицы друг к другу. Вот почему дополнительная инертность каждой частицы, связанная с их полевым взаимодействием, пропорциональна потенциальной энергии этого взаимодействия!

Полевая масса является физической величиной, характеризующей темп протекания изменений в системе. Чем сильнее связаны объекты системы посредством полевых взаимодействий, тем дольше протекают изменения, что выражается в увеличении их масс. Ветчина массы каждого объекта определяется потенциалом взаимодействия этого объекта с другими объектами.

Похоже, нам все-таки удалось пролить немного света на природу массы. Примечательно, что в классической и современной физике существует ряд примеров, которые приводят к аналогичному взгляду на массу. Одним из таких примеров может служить движение шара в идеальной жидкости, которое рассматривается в любом учебнике механики сплошных сред. Эта аналогия во многом похожа на наши представления о движении заряженной частицы со сферической оболочкой в полевой среде других частиц.

Уравнение движения шара массы m со скоростью и под действием некой силы F в пустоте имеет знакомый вид второго закона Ньютона:

Если же теперь этот шар движется в идеальной жидкости, то в уравнение движения добавляется сила сопротивления со стороны жидкости:

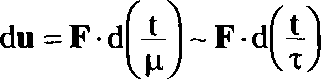(1.4.6)

(1.4.7)

29

где р — плотности жидкости, 1 - радиус шара. Эту формулу можно свести к движению шара в пустоте:

(m+n)^- = F (1.4.10)

если к обычной классической массе добавить так называемую присоединенную массу:

Ц = |л13р (1.4.11)

Таким образом, сопротивление жидкости свелось к появлению добавки к массе шара! Чем больше плотность жидкости или радиус шара, тем такое сопротивление больше. Или другими словами, интенсивнее взаимодействие шара с жидкостью, а значит, больше и добавка к массе. Этот пример наглядно показывает, как появление среды может сказываться на увеличении инерции тела.