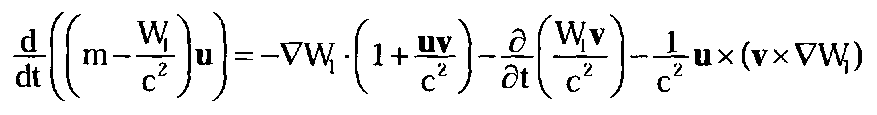(4.14.8)

Как мы уже знаем (выражение 4.2.12), сумму двух компонент массы в левой части уравнения движения можно представить в виде массы, зависящей от скорости по релятивистскому закону:

Это вносит в классическую силу Лоренца часть релятивистских поправок. Далее нам осталось представить величину \N{ в виде произведения заряда исследуемой частицы q на скалярный потенциал ф, созданный движущимся источником:

281

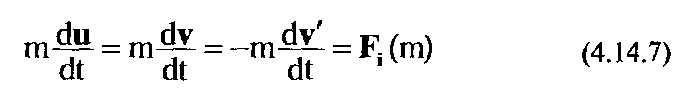(4.14.10)

А также ввести векторный потенциал:

(4.14.11)

Последнее слагаемое в уравнении (4.14.8) можно преобразовать по формуле:

После замены обозначений полевое уравнение движения (4.14.8) принимает окончательный вид:

Это и есть выражение для силы Лоренца, возникающее в полевой физике.

4.15. Экспериментальный метод

и математический формализм — еще один урок истории

В полученном нами уравнении есть все! Блеск и нищета классической электродинамики и теории относительности. Сущность всей концепции полевой среды и динамической массы. Итог пути, начатого нами в первой главе. Право сделать перерыв после длительного марафона к континенту полевой физики и по его просторам. Ощущение переломного момента в нашем путешествии, связанное с завершением первого этапа. И уверенность в твердости почвы под ногами. Перепишем полевое уравнение движения частицы регистрации под влиянием произвольно движущегося заряда-источника еще раз.

Полевая сила Лоренца

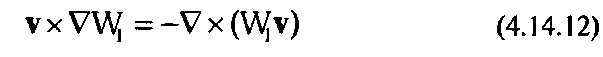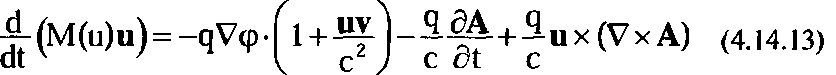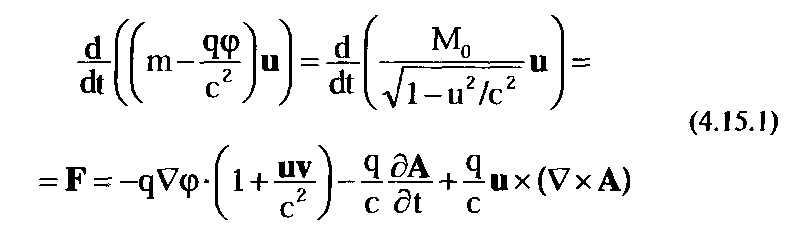282

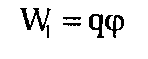Да, классическая сила Лоренца в этом уравнении вполне узнается. В правой части мы видим все знакомые из электродинамики слагаемые.

Например, силу в магнитном поле В = V х А :

Fm=%x(VxA) = ^UxB (4.15.2)

Вихревое электрическое поле:

F =_Ч5А 4 5 3)

с at ( }

Электростатическую силу:

F0=-qVcp (4.15.4)

А также соответствующую релятивистскому формализму левую часть уравнения движения с зависящей от скорости массой.

Однако в этом уравнении видно и нечто иное. То самое, чего не достает в классической электродинамике. Потерянное слагаемое, благодаря которому полевая сила Лоренца инвариантна к переходу в любую другую систему отсчета, а обычная сила Лоренца — нет. Это перекрестная поправка к электростатической силе:

F.=-qV9m = Fom (4155)

Именно из-за отсутствия этого слагаемого в формуле силы Лоренца вот уже более ста лет физика испытывает заметные затруднения. Вместо очевидных преобразований Галилея приходится использовать искусственные преобразования Лоренца. Возникает иллюзия сокращения длин и замедления времени при переходе из одной системы отсчета в другую. Существуют представления о неевклидовости пространства и много других неадекватных представлений. Просто страшно подумать о роли этого неприметного слагаемого в истории физики и всего нашего мировоззрения!