246

употреблять более привычный термин потенциальной энергии, потому что в данном случае это не создает серьезной путаницы.

И тем не менее, следует более детально определиться с производными механическими понятиями, такими как энергия, импульс и момент импульса. Что мы и готовы сейчас сделать. Как известно, логика появления этих величин в классической механике состоит в возможности проинтегрировать уравнение движения в общем виде и использовать в дальнейшем набор законов сохранения.

Один из интегралов полевого уравнения движения получить достаточно просто. Умножим уравнение движения:

на скорость и:

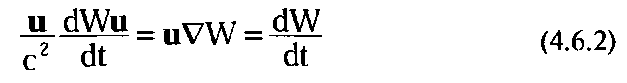и проинтегрируем получившееся выражение. Подобное уравнение мы уже интегрировали чуть выше (выражение 4.2.15) и видели, что его достаточно легко записать в виде полного дифференциала:

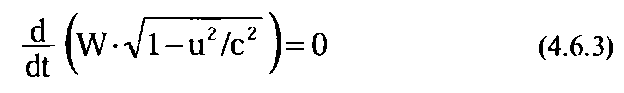А следовательно, в процессе движения частицы в полевой среде остается неизменной величина, стояшая в скобках, которую мы и назовем энергией.

Энергия является физической величиной, характеризующей движение частиц в полевой среде. Она остается неизменной в процессе движения и определяется выражением:

Е = wVl-u2/c2 = const (4.6.4)

На первый взгляд наше новое выражение для энергии выглядит достаточно непривычно. И обнаруживает ряд интересных свойств. Например, полная энергия движения всегда пропорциональна функции связи

частиц W. И вообще говоря, ее нельзя разделить на энергию движения (кинетическую энергию), связанную только со скоростью частицы, и потенциальную энергию. Как мы понимаем, это обстоятельство связано с тем, что полевая масса частицы — ядро энергии движения — также зависит от величины W.

247

При отсутствии всех взаимодействий W = 0 полная энергия частицы

тождественно равна нулю Е = 0. И она никак не связана со скоростью частицы! Это является подтверждением тех выводов, которые мы сделали о свободной частице в прошлой главе. В полевой физике изолированная частица лишена смысла, как и ее местоположение, скорость или энергия.

Далее новая формула для энергии еще раз подчеркивает то обстоятельство, что в полевой среде скорость относительного движения частиц не может превысить скорость распространения возмущений с. Причем точка покоя и = 0 соответствует минимальному по абсолютной величине значению потенциала W. Рост скорости частицы приводит к уменьшению радикала и требует роста абсолютной величины потенциала. В области бесконечных значений функции W частица может разогнаться до предельной скорости с. При этом в области малых значений