Результат последнего этапа, еще более увеличенный, демонстрирует мельчайшие детали в виде очень тонких, едва видимых выступов, которых вы, конечно же, не увидели бы, не обладай наша графическая система такой превосходной разрешающей способностью.

Как в терагонах, так и в предельной кривой отсутствует какое бы то ни было самоперекрытие, самопересечение или самокасание. Это утверждение остается в силе и для последующих построений (вплоть до рис. 85).

< Не следует забывать о том, что фракталы на рис. 81-85 представляют береговые линии; суша и море здесь — это удобные фигуры, обладающие положительными и конечными площадями. На с. 209 упоминается случай, в котором только «море», будучи объединением простых трем, имеет вполне определенную площадь, в то время как суша не имеет ни единой внутренней точки. ►

Тайлинг и пертайлинг. Этот остров можно разбить на 16 меньших островков (г = 1/4). Каждый представляет собой остров Коха, построенный на одном из 16 квадратов, образующих первый этап построения.

< В главах 25 и 29 показано, что размерность £> = 3/2 характерна также для многих броуновских функций. Следовательно, это значение легко можно получить с помощью случайных кривых и поверхностей. ►

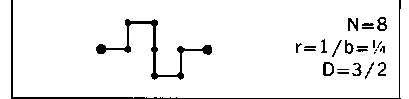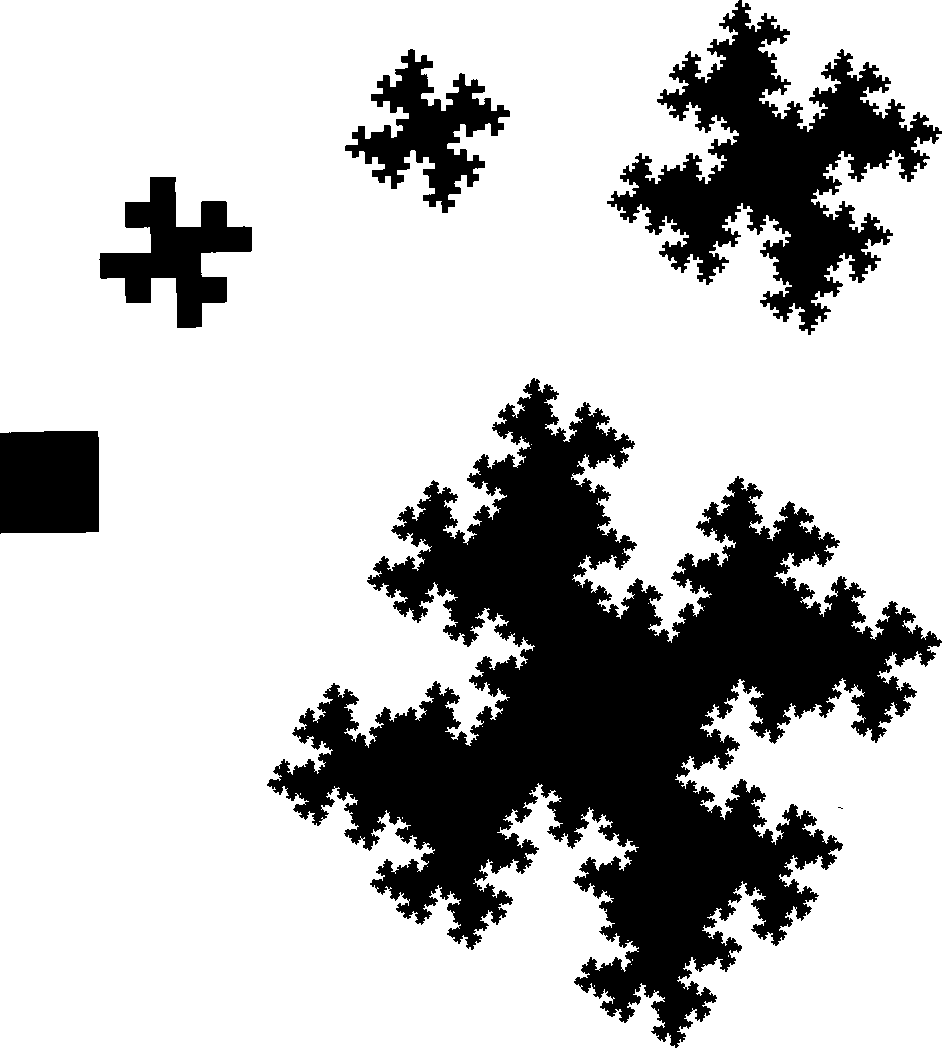Рис. 83. КВАДРАТИЧНЫЙ ОСТРОВ КОХА (РАЗМЕРНОСТЬ БЕРЕГОВОЙ ЛИНИИ £> = 1п18/1п6 ~ 1,6131)

В качестве инициатора снова возьмем квадрат, а генератором будет следующая ломаная:

То, что береговая линия квадратичных островов Коха, представленных в данной подборке иллюстраций, в очень значительной степени зависит от D, весьма показательно. В то же время, поскольку их общим инициатором является квадрат, внешняя форма этих островов остается приблизительно одинаковой. Если инициатором выступает какой-либо другой правильный М-угольник (М > 4), то можно наблюдать, как по мере увеличения М внешняя форма становится все более гладкой. Об истинной зависимости между внешней формой и значением D мы узнаем не раньше, чем в главе 28, в которой рассматриваются случайные береговые линии, эффективно определяющие как генератор, так и инициатор.

< Максимальность. Свой вклад в сходство внешних форм вносит тот факт, что изображенные на рис. 79-85 квадратичные кривые Коха обладают весьма интересным свойством максимальности. Расположим все генераторы Коха, порождающие кривые без самопересечений, на квадратной решетке, образованной прямыми, параллельными и перпендикулярными отрезку [0, 1]. Допустим также, что все эти генераторы можно использовать с любыми инициаторами на нашей квадратной решетке. Определим как максимальные те генераторы, которые характеризуются наибольшим значением N и, как следствие, D. Нетрудно заметить, что TVmax = Ь2/2 при четных Ь и TVmax = (b2 + 1)/2 при нечетных Ь.