Евклидова размерность плоскости равна 2. Отсюда аналогичным образом следует, что при любом значении Ь «целое», состоящее из прямоугольника с длинами сторон 0^1<1иО^)/<Г, может быть без остатка «разбито» на N = Ь2 частей. Части эти представляют собой прямоугольники, определяемые системой уравнений

где к и Ь, изменяются от 1 до Ъ. И здесь каждая часть может быть получена из целого с помощью преобразования подобия с коэффициен-

РАЗМЕРНОСТЬ ПОДОБИЯ

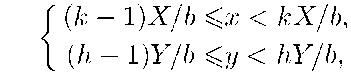том г(ЛГ) = 1/6= г/и1/2.

64

Три классических фрактала — совершенно ручные о II

В случае прямоугольного параллелепипеда аналогичное рассуждение приводит нас к коэффициенту г (ТУ) = 1 /ТУ1/3.

Не возникает никаких сложностей и с определением пространств, евклидова размерность Е которых больше 3. (Здесь и далее мы будем обозначать евклидову — или декартову — размерность буквой Е.) Для всех ТЗ-мерных параллелепипедов (И < Е) соблюдается равенство

г (ТУ) =

Таким образом, ЛГ п

1\г = 1.

Эквивалентные альтернативные выражения имеют следующий вид:

1пг(ТУ) =1п(1/7У1/д) = -(1пЛ0/£>, £> = — 1п ТУ/ 1п г (ТУ) = 1пТУ/1п(1/г).

Перейдем теперь к нестандартным фигурам. Для того, чтобы показатель самоподобия имел формальный смысл, необходимо лишь, чтобы рассматриваемая фигура была самоподобной, т. е. чтобы ее можно было разбить на Лг частей, каждая из которых может быть получена из целой фигуры с помощью преобразования подобия с коэффициентом г (в сочетании со смещением или преобразованием симметрии). Полученная таким образом величина £) всегда удовлетворяет равенству

О < £> < Е.

В случае троичной кривой Коха N = А, а г = 1/3, отсюда £> = 1п 4/ 1п 3, что полностью совпадает с хаусдорфовой размерностью.

КРИВЫЕ. ТОПОЛОГИЧЕСКАЯ РАЗМЕРНОСТЬ

До сих пор мы, не особенно задумываясь, называли фигуру Коха /С кривой; настало время разобраться с этим понятием. Здравый смысл подсказывает, что стандартная дуга представляет собой связное множество, причем если удалить любую его точку, то множество становится несвязным. А замкнутая кривая — это связное множество, разделяющееся после удаления двух точек на две стандартные дуги. По этим причинам фигуру Коха /С можно считать кривой.