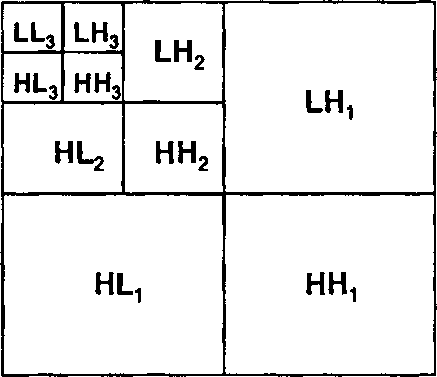Рис. 7.2.1. Структура вейвлет-поллерева. Шх обозначает композицию верти-

кального высокочастотного и горизонтального низкочастотного операторов, а Ніх - композицию вертикального низкочастотного и горизонтального высокочастотного операторов

Еще раз остановимся на обозначении композиции операторов: ЬНХ, например, означает, что первым применятся оператор Нх, а затем к результату - оператор Ь.

7. Технологии вейвлет-сжатия изображений

187

Смысл введения структуры дерева в том, что, как правило, коэффиц^щъ1_Г1 блоках на различных уровнях обладают значительной степенью прдобщ. То есть дочерние коэффициенты на некотором уровне, вероятно, будут похожими на своих «родителей», находящихся на предыдущем уровне. Это очевидно из примеров, представленных на Рис. 5.8.2 в главе 5 и на Рис. 7.2.3, показанном ниже. В частности, довольно распространен случай, что если коэффициент квантуется до нуля, то и его дочерние коэффициенты тоже квантуются до нуля. Это наблюдение легло в основу так называемого вейвлет-кодирования с нуль-деревом (wavelet zerotree encoding), впервые примененного Льюисом и Ноулесом (Lewis и Knowles) [25].

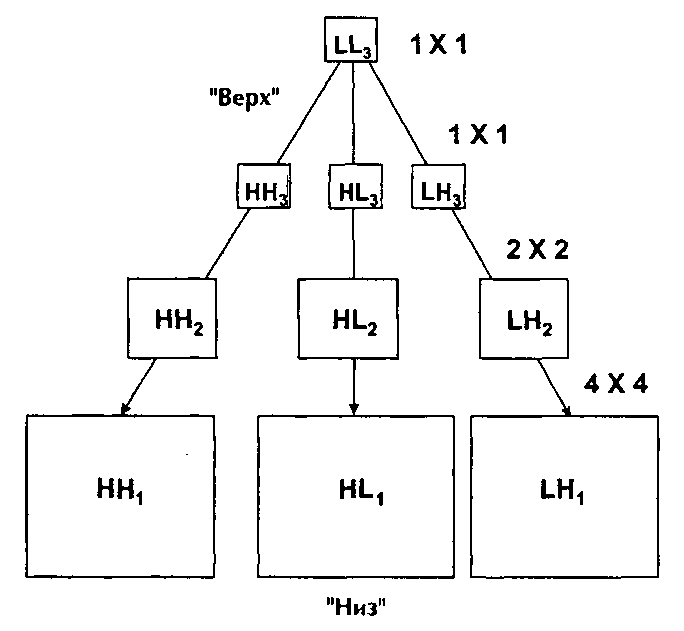7.2.2.

Блоки вейвлет-поллерева с Рис. 7.2.1 упорялочены злесь в структуру лерева. Кажлый коэффициент в блоке имеет четыре лочерних, располагающихся в соответствующих блоках слелуюшего уровня. Например, если Рис. 7.2.1 прелставляет вейвлет-преобразование изображения 8x8, то іі3, НН3, Н13 и ІН3 - это блоки 1 х 1, НН2, Ні2, и Ш2 - блоки 2x2 и НИь и Ш1 - блоки 4x4. «Верх» и «низ» отмечены, поскольку эти термины используются в алгоритме нуль-лерева, описанном ниже

188

Рис. 7.2.3. Изображение «Lena» (а) и его венвлет-преобразование (Ы. Изображе-

ние на Рис (Ь) состоит из 50% наибольших вейвлет-коэффиинентов Хаара, прорисованных черным цветом. На нем нанесена структур вейвлет-поллерева с обозначенными на ней некоторыми высокочастотными и низкочастотными операторами. Обратите внимание на полобие соответствующих блоков на соселних уровнях

В оригинальной реализации вейвлст нуль-дерева Льюиса и Ноулеса [25] 0 сопоставляется всем потомкам коэффициентов, квантуемых до нуля. Этот метод можно рассматривать, как вид кодирования длин последовательностей (runlength coding) Фактически он гораздо эффективнее традиционного кодирования длин последовательностей, так как в нем не требуется кодирования длины последовательности нулей. Однако, хотя действительно, что те коэффициенты в структуре поддерева, которые квантуются до нуля, вероятно, будут иметь потомков, которые тоже квантуются до нуля, так же вероятно и что они будут иметь значимых ненулевых потомков Эта возможность привносит ошибки в метод нуль-дерева Льюнса и Ноулеса. Шапиро (Shapiro) [41] предложил модифицированный метод кодирования с нуль-деревом, которын учитывает возможность изолированных нулей. Сейд и П№ ман (Said и Pearlman) [36] и [37] предложили усовершенствованный вариант кодирования с нуль-деревом, названный «разбиение множества в иерархических деревьях» (Set Part1" tioning in Hierarchical Trees - SPIHT). В следующей главе подробно рассмотрим реализацию кодирования с н>лЬ" деревом, подобную методам, предложенным Шапиро и Сеулом и Пилманом.