Фракталы - это красиво!!!

 

Впервые я услышал о них в 1988 году, от профессора Тартуского университета Славина, тогда информации по ним было очень мало. Он составил программу на Бейсике (язык программирования такой) для домашнего отечественного компьютера БК 0010 и получил  изображения множества Мандельброта. Вот тогда они меня и покорили. Их красота и загадочность...

Не вдаваясь в математические тонкости можно сказать, что фракталы это самоподобные структуры. Т.е. взяв отдельную часть изображения фрактала, можно в ней обнаружить все тоже самое, что и в основном изображении. Возможно это не совсем корректное объяснение, но это так. Простейший пример фрактальной структуры в природе является линия морского берега, многие естественные границы, которые становятся явно тем длиннее, чем более мелкий масштаб используется для их измерения. Границы такого рода в математике называют множествами Жулиа (Julia)

Из этого множества, математически можно выделить (изменяя параметры) самое необычное множество Мандельброта. (Mfndelbrot)

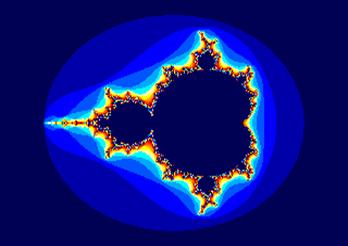
Главная особенность тих фрактальных структур состоит в том, что мы можем выбрав область на изображении множества, «увеличить» её, получая при этом новое красивейшее изображение.

Существует несколько известных программ для генерации фракталов, рассмотрим некоторые из них.

Своим появлением на свет и популярностью фракталы обязаны математику Бенуа Мандельброту. Заслуга Б. Мандельброта в том, что ему удалось собрать вместе, назвать и сделать всеобщим достоянием разрозненные сведения, первое появление которых относиться к началу XX века. Сначала существовавшие как плод воображения математиков, фракталы были найдены в реальных объектах окружающего мира. Очертания гор, границы материков, русла горных рек, береговая линия и многое другое - все это фракталы.

Что же такое фракталы? Часто, говоря о них, имеют в виду фрактальную кривую, обладающую нецелой (дробной) размерностью (1<D<2). Таким образом, фрактальная кривая – это геометрический объект, объединяющий в себе свойства линии и плоскости, в тоже время не являющийся ни тем, ни другим. Обратимся к классическому примеру, приведенному  Мандельбротом и ставшим уже классическим: рассмотрим береговую линию, которая представляет собой типичный фрактал. При попытке измерить её длину окончательный результат будет меняться в зависимости от масштаба единицы измерения. Полученная закономерность заключается в том, что измеренная длина береговой линии будет увеличиваться с уменьшением длины измерительного прибора. Зависимость увеличения измеренной длины контура от уменьшения длины измерительного прибора называется фрактальной размерностью.

Береговая линия, в зависимости от её изрезанности, может иметь разное значение фрактальной размерности: при малой изрезанности размерность прилижется к 1, при большей к 2. Фрактальная кривая размерностью, близкой к 2, фактически заполняет пространство и становится полосой.

Наиболее известными фрактальными объектами, появившимся задолго до самого слова "фрактал", можно назвать кривую Коха (аналог в природе - снежинка),

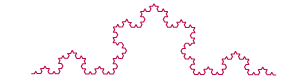
 треугольную и универсальную кривую Серипнского, фигуру Лихтенберга, появляющаяся в виде узора на пластинке диэлектрика после его пробоя.

Наиболее простой программой генерации множества Мандельброта является -  INFI разработанной Mikko Poyhonen  в 1997 году. Запустив программу, сразу наблюдаем множество Мандельброта в красивейших зеленых тонах. Интерфейс программы интуитивно понятен: стандартные для Windows меню File, View, Fractal, Window, Help. Из общего ряда выделяется только меню Fractal. В нем задаются режимы программы Zoom (Увеличение), Pan (Перемещение изображения), Rotate pallete (Ротация палитры цветов). С помощью последней опции можно изменять цветовую гамму множества. Интересной особенностью программы является музыкальное сопровождение путешествия в мир фракталов (Play mode). В меню View есть вкладка Properties (Свойства) она, кстати, автоматически раскрывается при запуске программы. В ней задаются координаты, Max Iters (количество итераций) этот параметр очень важен так как он позволяет более четко прорисовывать картинку. Параметр Bail out изменяет плавность цветовых переходов. Во вкладке Pallete есть уже готовые варианты палитр, там же можно записать свой вариант, сделать ротацию цветов фона или самого изображения. Программа позволяет выставлять разрешения от самого простого 320x200 до 1024x768. Есть возможность делать закладки (меню Bookmarks) сохраняя параметры понравившегося изображений, конечно можно сохранять на диске и сами изображения в формате GIF или BMP.

В целом программа очень хороша для начинающих путешественников в мир фракталов.

Загрузить ее можно здесь: http://www.hut.fi/~mpoyhone/infi/

 Одна из самых знаменитых программ FRAINT. Созданная сообществом программистов, она распространяется как Freeware. Эта программа обладает самыми богатыми возможностями.  Позволяет даже строить фракталы в 3-х измерениях. Интерфейс её достаточно понятен. Есть демо - режим. Единственный её недостаток,  работает она под  MS-DOS. (хотя, впрочем? работает в DOS окне под Windows)

Скачать программу можно отсюда : http://spanky.triumf.ca/www/fractint/fractint.html

Еще одна неплохая программа создания изображений фракталов - Ultra Fractal. В отличие от других программ, Ultra Fractal позволяет создать вашу формулу фрактала, используя встроенный редактор формул. Программа работает очень быстро, используя оптимизированный код. Можно также накладывать изображения, используя слои. Слои можно вращать, увеличивать, использовать заливку. Вообще стоит посмотреть: http://www.ultrafractal.com

Литература

[1] Бондаренко В.А.,Дольников В.Л. Фрактальное сжатие изображений по Барнсли-Слоану. // Автоматика и телемеханика.-1994.-N5.-с.12-20.
[2] Витолин Д. Применение фракталов в машинной графике. // Computerworld-Россия.-1995.-N15.-с.11.
 [3] Федер Е. Фракталы. Пер. с англ.-М.: Мир,1991.-254с. (Jens Feder, Plenum Press, NewYork, 1988).
 [4] Шабаршин А.А., Введение во фракталы. 1998. Екатеринбург.
 [5] Х.-Щ. Пайтген, П.Х. Рихтер Красота фракталов; Пер. с англ.-М  Мир 1993.
 [6] Michael F. Barnsly The Desktop Fractal Design Handbook, 1989, Boston, Academic Press, Inc.