Однако ничтожное трение на льду может быть успешно использовано технически. Уже обыкновенные сани служат тому примером. Еще лучше свидетельствуют об этом так называемые ледяные дороги, устраиваемые для вывозки леса с места рубки к железной дороге или к пунктам сплава. На такой дороге, имеющей словно гладкие ледяные рельсы, две лошади тащат сани, нагруженные 70 тоннами бревен (рис. 22).

ФИЗИЧЕСКАЯ ПРИЧИНА КАТАСТРОФЫ „ЧЕЛЮСКИНА"

Из сказанного сейчас не следует делать поспешного вывода, что трение о лед ничтожно при всяких обстоятельствах. Даже при температуре, близкой к нулю, трение о лед бывает нередко довольно значительно. В последние годы, в связи с работой наших ледоколов, тщательно изучалось трение льда полярных морей о стальную обшивку корабля. Оказалось, что оно неожиданно велико, не меньше трения железа по железу: коэфициент трения новой стальной судовой обшивки о лед равен 0,2.

Чтобы понять, какое значение имеет эта цифра для судов при плавании во льдах, разберемся в рисунке 23; он изображает направление сил, действующих на борт MN судна при напоре льда. Сила Р давления льда разлагается

40

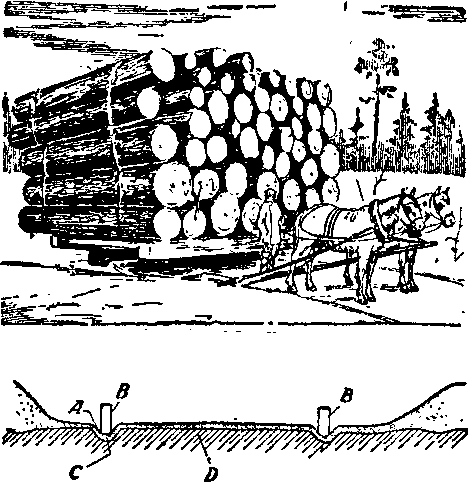Рис. 22. Вверху — нагруженные сани на ледяной дороге; две лошади везут 70 т груза. Внизу—ледяная дорога: А — колея; В—полоз; С—уплотненный снег; D — земляное основание дороги.

Рис. 23. „Челюскин", затертый во льдах. Внизу: силы, действующие на борт MN судна при напоре льда.

на две силы: R—перпендикулярную к борту, и F— направленную по касательной к борту. Угол между Р и R равен углу а наклона борта к вертикали. Сила Q трения льда о борт равна силе R, умноженной на коэфициент трения, то-есть на 0,2; имеем Q = 0,2 R. Если сила трения Q меньше F, последняя сила увлекает напирающий лед под воду; лед скользит вдоль борта, не успевая причинить судну вреда. Если же сила Q больше F, трение мешает скольжению льдины, и лед при продолжительном напоре может смять и продавить борт.

Когда же Q<^F? Легко видеть, что F=Rtga; следовательно, должно существовать неравенство: Q<CRtga'$ а так как Q = 0,2/?, то неравенство Q<C.F приводит к другому:

0,2/?</?tga,

или

tg«>0,2.

По таблицам отыскиваем угол, тангенс которого 0,2; он равен 11°. Значит Q<^F тогда, когда <х>11°. Тем самым определяется, какой наклон бортов корабля к вертикали обеспечивает безопасное плавание во льдах: наклон должен быть не меньше 11°.