at dt

(1.8.1)

В этой формуле тир — классическая и полевая массы исследуемой частицы, и — ее скорость в лабораторной системе, v — скорость частицы-источника, R — расстояние между частицами. Угловая скорость СО вращения системы поля, связанной с источником, относительно лаборатории выражается через другие величины по формуле:

Rx(u-v) Rxu Rxv

©=-S-- = ^2TL-^VL = G>n-<Bv (1.8.2)

R R R

в которой мы разбили угловую скорость на две части. Так ©>„ зависит только от скорости частицы регистрации, а соу — от скорости источника.

После замены полевой массы р. ее значением:

(1.8.3)

45

где q - заряд исследуемой частицы, а ф — потенциал, созданный частицей-источником, выражение для силы приобретает более близкий к силе Лоренца вид:

(1.8.4)

Сейчас мы не будем стремиться привести эту формулу к известному виду силы Лоренца. Начнем с малого и будем по очереди «вынимать» из написанной формулы понятные нам слагаемые, а потом посмотрим, какой смысл несут в себе остальные члены.

Начнем с наиболее очевидной составляющей — силы Кориолиса. В написанных выше формулах она имеет вид:

(1.8.5)

По своей структуре сила Кориолиса аналогична магнитной силе — пропорциональна скорости частицы регистрации и перпендикулярна ей. Более того, после замены полевой массы ее выражением, аналогия становится полной! Вектор магнитного поля определяется условием:

(1.8.6)

Подставим теперь в эту формулу значение угловой скорости, причем возьмем пока только ту ее часть СО = —C0V , которая определяется скоростью движения источника. Также заменим величину потенциала ф, созданного точечным источником с зарядом Q на расстоянии R , его значением ф = Q/R . В результате мы получаем известное выражение для магнитного поля, созданного движущимся зарядом:

(1.8.7)

Если же речь идет об однообразном движении множества источников, например тока в проводнике, то мы приходим к сумме:

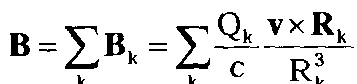(1.8.8)

или переходя к непрерывному распределению заряда dQ = pdV с объемной плотностью р и интегралу:

в=да™ «ад

V

где j = pv — вектор плотности тока.

Мы получили формулу Био-Савара для выражения магнитного поля, исходя исключительно из механистических соображений! Из обычных сил инерции!