Поняв принцип работы этого выражения, применим его к написанию силы Лоренца в лабораторной системе отсчета. Классические силы инерции в этой системе отсутствуют. Зато к обычной электростатической силе F0 добавляются все полевые силы инерции, определяемые полевой массой \х:

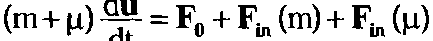(1.7.15)

42

Это выражение можно получить и из более формальных соображений. Если полная масса частицы регистрации равна m + Ц , то в системе поля обычное классическое уравнение движения запишется в виде:

(m+n)-a0=F0+F.n(m) (1.7.17)

Умножая формулу связи ускорений (1.7.14) на ц, мы получим соотношение:

Ца = ца0+Ц„(ц) (1.7.18)

Аналогичная связь ускорений существует и для обычной инерции массы m, только знак сил инерции обратный — они возникают не при переходе из системы поля в лабораторную систему, а наоборот:

ma0 = ma + Fin(m) (1.7.19)

Исключая из этих трех соотношений а0 и Fta (m), мы получаем для лабораторной системы:

ma + na = F0+Fin(n) (1.7.20)

что полностью соответствует написанной выше формуле (1.7.16). Впрочем, пока нам важно уловить только суть подхода, а впоследствии мы строго выведем это правило комбинации сил инерции из формул динамики полевой среды.

Разобравшись с уравнением движения пробной частицы, мы совсем близко подошли к желаемой цели. Чтобы в полученном нами выражении (1.7.16):

I \ du , <3(v + G>xR)

(m+|n)^H- = F0 + |Li—-——---|huxg>-|hg>x(v+g>xR)

(1.7.21)

стала легко узнаваться сила Лоренца, нужно заменить полевую массу (ц, обусловленную взаимодействием двух заряженных частиц, ее выражением:

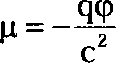(1.7.22)

где q - заряд частицы регистрации, ф - потенциал, созданный частицей-источником, С — константа скорости света. Вместо электростатической силы также подставим ее значение согласно формуле Кулона:

F0=-qV9 (1.7-23)

43

В результате мы получаем долгожданную формулу:

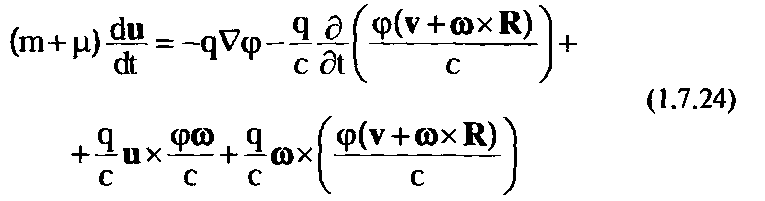Как мы и подозревали заранее, она оказалась далекой от идеала, и над ней надо еще работать и работать.

Однако многое уже становится ясно. Проделанная работа оказалась не напрасной, и это служит подтверждением правильности выбранного нами пути. Так первое слагаемое в правой части, разумеется, есть обычная электростатическая сила. Во втором слагаемом просматривается вихревое электрическое поле: