Анонс. В главе 22 мы воспользуемся фрактальными инструментами для улучшения нашего понимания смысла космологического принципа, рассмотрим, как его можно и нужно модифицировать, и узнаем, почему такая модификация непременно требует случайности. Обсуждение скоплений в рамках усовершенствованной модели мы отложим до глав 22, 23 и с 32 по 35.

МОЖНО ЛИ ГОВОРИТЬ О ГЛОБАЛЬНОЙ плотности

Начнем с тщательного рассмотрения концепции глобальной плотности материи. Как и в случае береговых линий, здесь все, на первый взгляд, выглядит очень простым, однако на деле очень быстро — и весьма интересно — запутывается. Для определения и измерения плотности начинают с массы М (Н), сосредоточенной внутри сферы радиуса К с центром, совпадающим с центром Земли. Так оценивается приблизительная плотность, определяемая как

После этого величину К устремляют к бесконечности, а глобальная плотность определяется как предел, к которому сходится в этом случае приблизительная плотность.

Однако обязательно ли глобальная плотность сходится к положительному и конечному пределу? Если так, то скорость такого схождения

МАТЕРИИ?

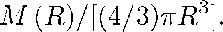9 о Фрактальный взгляд на скопления галактик

і:

оставляет желать лучшего, и это еще мягко сказано. Более того, оцеш предельной плотности, будучи рассмотрены во временной перспектиЕ ведут себя довольно странно. По мере того как увеличивалась глуб на наблюдаемой в телескоп Вселенной, приблизительная плотность ] удивление систематически уменьшалась. Согласно де Вокулеру [104], уменьшение всегда было ос Н°~3. Наблюдаемый показатель В мно меньше 3 — в наилучшем приближении £) = 1, 23.

Де Вокулер выдвинул тезис о том, что поведение величины прибл зительной плотности отражает реальность, имея в виду, что М (Д)осД Эта формула вызывает в памяти классический результат для шара рад уса К, вложенного в евклидово пространство размерности Е, — объс такого шара ос НЕ. В главе 6 мы встречались с такой же формуле для кривой Коха, с той лишь разницей, что показателем там была ] евклидова размерность Е = 2, а дробная фрактальная размерность 1 А в главе 8 мы получили формулу М (К) ос Я0 для канторовой пьи на временной оси (здесь Е = 1).