< А если совсем позабыть о дисциплине, то мы почти наверняка не получим ничего, кроме бесконечно повторяющихся самопересечений, поскольку полностью недисциплинированная кривая Пеано — это броуновское движение, о котором мы уже упоминали во второй главе и поговорим подробнее в главе 25.

< Теорема Лиувилля и эргодичность. В механике принято представлять состояние сложной системы одной-единственной точкой

в «фазовом пространстве». Известно, что в случаях применения к этому пространству уравнений движения каждая его область ведет себя следующим образом: ее протяженность (гиперобъем) остается инвариантной (теорема Лиувилля), однако ее форма меняется — область рассеивается и заполняет весь доступный объем с максимально возможной однородностью. Очевидно, что оба этих свойства находят отражение в том, как, с нашей легкой руки, ведет себя черный квадрат при построении кривой Пеано. Представляется интересным «копнуть» глубже и увидеть, что во многих упрощенных «динамических» системах, допускающих подробное изучение, каждая область рассеивается, трансформируясь во все удлиняющуюся и утончающуюся ленту. Интересно также было бы выяснить, не происходит ли дисперсия других систем по древовидным кривым Пеано вместо лент. ►

Рис. 98 и 99. КВАДРАТИЧНЫЕ ПОСТРОЕНИЯ КОХА С РАЗМЕРНОСТЬЮ D = 2: ПРОХОЖДЕНИЯ ТРЕУГОЛЬНИКА ПО ЧЕЗАРО И ПО ПОЙА И ИХ ВАРИАНТЫ

Простейшим генератором, какой только можно в этом случае вообразить, является ломаная, состоящая из N = 2 равных отрезков, угол в между которыми удовлетворяет условию 90° ^ в ^ 180°. В предельном случае в = 180° генератор представляет собой отрезок прямой; случай в = 120° (проиллюстрированный в пояснении к рис. 71) порождает (помимо прочих) троичную кривую Коха. Генератор для предельного случая в = 90° показан ниже:

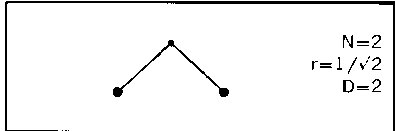Используя этот генератор, можно построить невообразимое множество различных кривых Пеано (различия обусловлены формой инициатора и способом помещения генератора на предшествующий терагон). На рис. 98-102 дано несколько примечательных примеров.

< Кроме того, в главе 25 с помощью рандомизации всех кривых Пеано с данными N г мы получим самое что ни на есть броуновское движение. ►