Авторы работы [313] невольно сделали значительный вклад во фрактальную геометрию, попытавшись заполнить КЕ шарами, радиус каждого из которых имеет вид рк = рогк, где г < 1; число шаров радиуса рк на единицу объема имеет вид Пк = по^к, где и — целое число вида V = (1 — г)г~Е, что накладывает жесткие ограничения на г. Таким образом, показатель распределения размеров пустот определяется

204

Масштабно-инвариантные фракталы о IV

следующим выражением:

Сначала разместим большие сферы радиуса р\ в центрах ячеек решетки с шагом 2р\. Узлы решетки с шагом 2р2, лежащие вне больших сфер, оказываются достаточно многочисленными, чтобы послужить центрами для сфер меньшего радиуса (рг) и так далее. Такая конструкция подразумевает следующие верхние границы величины г:

Заполнение К непересекающимися шарами может занять меньшее время. В случае же одномерной линии максимальное значение г составляет 1/3, что соответствует значению г для троичной канторовой пыли! Существование канторовых пылевидных множеств с г > 1/3 указывает на то, что одномерная упаковка может оставлять пустоты произвольно малой размерности. С другой стороны, более тесная упаковка подразумевает более сложную структуру.

Даже после того, как мы добавим к размерностям Ет и £> степень ветвления Д, фрактал остается во многих отношениях недостаточно определен. Особое значение имеет еще одно дополнительное свойство, которое я назвал лакунарностью. Пустоты в очень лакунарном фрактале имеют очень большой размер, и наоборот. Основные определения можно было бы привести и здесь, однако мне представляется более целесообразным отложить это до главы 34.

Рис. 205. СТРЕЛА СЕРПИНСКОГО (РАЗМЕРНОСТЬ ГРАНИЦЫ £> ~ 1,5849)

В [522] Серпинский строит кривую, инициатором которой является интервал [0, 1], а генератор и второй терагон выглядят следующим

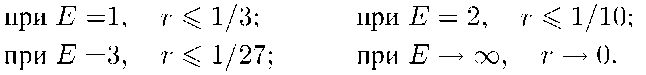АНОНС: ЛАКУНАРНОСТЬ

образом:

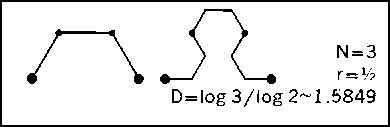Последующие этапы построения имеют вид:

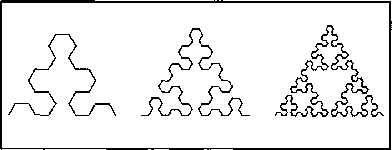О том, как будет выглядеть эта кривая на одном из поздних этапов построения, можно получить представление, взглянув на очертания «береговой линии» в верхней части рис. 205 (над самым большим черным тр еугольником).